obliczenie pola zacieniowanego obszaru mort: Witam Mam problem z takim oto zadankiem : prosta AB jest wspólna styczną okręgów x² + y² = 16 i (x−16) ² + y² = 144 .Oblicz pole zacieniowanego obszaru .

ICSP: a ten zacieniowany obszar to ?

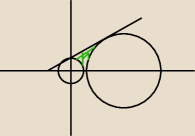mort: wygląda to mniej wiecej tak ... obszar , to jest ten zielony

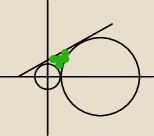mort: obszar , to to zaznaczone na zielono

mort: to jak , pomoże Ktoś ?

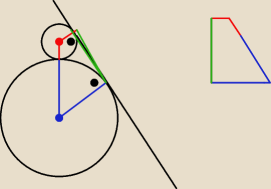ICSP: Teraz mam nadzieję ze zobaczysz tutaj trapez Aby policzyć pole zacieniowanej części wystarczy od Pola trapezu odjąć pola wycinków kół 1. Liczysz wysokość trapezu 2. Liczysz pole trapezu 3. Liczysz pozostałe dwa katy trapezu 4. Liczysz pole pierwszego wycinka 5. Liczysz pole drugiego wycinka Pole zacieniowenej figury = Pole trapezu − (Pole pierwszego wycinka + Pole drugiego wycinka) =

	88
= 128√3 −		π o ile nigdzie się nie pomyliłem
	3

mort: "Łebski" z Ciebie Gość widziałem ten trapez , tylko jedno z pól wycinka nie mogłem obliczyc (tego większego koła ) nie ma podanych żadnych kątów więc jak to obliczyłes ?(to , co na niebiesko ) aha , wynik podany w odp. w książce , to 64 √3 − 29 ¹₃ π

ICSP:

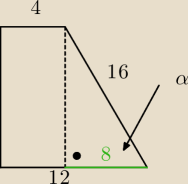
	8		1
cosα =		=		⇒ α = 60o
	16		2

Z resztą nie powinno być problemów Znalazłem też bład w moich obliczeniach

	88
odp taka jak w książce : 64√3 −		π
	3