awd awd: Dany jest prawidlowy ostroslup czworokatny. Pole przekroju plaszczyzna przechodzaca przez przekatna podstawy i rownolegla do krawedzi bocznej skosnej wzgledem tej przekatnej jest rowne P. Pole przekroju p laszczyzna przechodzaca przez srodki dwoch sasiednich bokow podstawy i srodek wysokosci ostroslupa wynosi S. Oblicz iloraz P S .

awd: pomoże ktoś ?

dero2005:

	H
KO = KW =
	2

	d
ON = NC =
	4

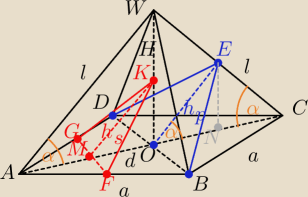
d = a√2

	a
FG =		√2
	2

H = dtgα h_s = √(^d₄)² + (^H₂)²

	GF*hs
S =
	2

	d
NC =		tgα
	4

h_p = √NC² + (^d₄)²

	d*hp
P =
	2

awd: Wielkie dzieki ! nigdy bym tego nie narysowal

Vizer: Po pierwsze, rozumiem uciechę, bo zadanie pochodzi z konkursu (Diamentowy Indeks AGH), więc jak się nie umiało zrobić, to najlepiej rzucić na forum i zostawić komuś mądrzejszemu do rozwiązania. Po drugie, wydaje mi się, że nie do końca zadanie zostało dobrze zrobione (całe szczęście), a chodzi mi o część z polem S, na rysunku jest tylko jakby jego fragment, bo cały przekrój (jeśli dobrze to sobie narysowałem) to będzie pięciokąt (jeszcze nie wiem czy foremny, bo jestem w trakcie główkowania). Po trzecie, prośba do Jakuba, przydałoby się zrobić albo jakąś nową podstronę albo w formie podwieszenia tematu, by były umieszczone tam w danej chwili jakie konkursy się odbywają by każdy pomagający wiedział, że takiego zadania nie można zrobić. Aha i żeby nie było, jestem na studiach, więc nie trafiłem tutaj w celu znalezienia rozwiązania, ale z czystej ciekawości.

Vizer: up

Bogdan: Zgadzam się z Vizerem, nie powinno się tu zamieszczać zadań z aktualnie prowadzonych konkursów oraz − powtórzę za Vizerem − na szczęście, zadanie nie zostało poprawnie rozwiązane.

Rafalo: Mi z moich obliczeń wyszedł stosunek równy 4/5.