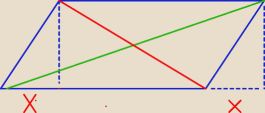
 H = 4 − wysokość graniastosłupa
a , b − długości boków równoległoboku; a > b
h − wysokość równoległoboku
p1 = √33 − długość krótszej przekątnej
p2 = 9 − długość drugiej przekątnej
Mamy
c2 + H2 = 92 = 81
d2 + H2 = (√33)2 = 33
czyli
c2 + 16 = 81 ⇒ c2 = 65
c = √65 ≈ 8,1 − długość dłuższej przekątnej równoległoboku
−−−−−−−−−−−−−
d2 + 16 = 33 ⇒ d2 = 17
d = √17 ≈ 4,1 − długość krótszej przekątnej równoległoboku
−−−−−−−−−−−−−−−−−−−−−
Mamy
( a + x)2 + h2 = c2 = 65
( a − x)2 = h2 = d2 = 17
2a + 2b = 18 ⇒ a + b = 9 ⇒ b = 9 − a ⇒ b2 = 81 − 18a + a2
x2 + h2 = b2 = 81 − 18a + a2
zatem
a2 + 2ax + x2 + h2 = 65
a2 − 2ax + x2 + h2 = 17
−−−−−−−−−−−−−−−−−−−−−−−−−−− dodajemy stronami
2a2 + 2*( x2 + h2) = 82 / : 2
a2 + x2 + h2 = 41
więc po podstawieniu 81 − 18a + a2 za x2 + h2 otrzymamy
a2 + 81 − 18a + a2 = 41
2a2 − 18a + 40 = 0
a2 − 9a + 20 = 0
−−−−−−−−−−−
Δ = 81 − 4*1*20 = 1
H = 4 − wysokość graniastosłupa
a , b − długości boków równoległoboku; a > b
h − wysokość równoległoboku
p1 = √33 − długość krótszej przekątnej
p2 = 9 − długość drugiej przekątnej
Mamy
c2 + H2 = 92 = 81
d2 + H2 = (√33)2 = 33
czyli
c2 + 16 = 81 ⇒ c2 = 65
c = √65 ≈ 8,1 − długość dłuższej przekątnej równoległoboku
−−−−−−−−−−−−−
d2 + 16 = 33 ⇒ d2 = 17
d = √17 ≈ 4,1 − długość krótszej przekątnej równoległoboku
−−−−−−−−−−−−−−−−−−−−−
Mamy
( a + x)2 + h2 = c2 = 65
( a − x)2 = h2 = d2 = 17
2a + 2b = 18 ⇒ a + b = 9 ⇒ b = 9 − a ⇒ b2 = 81 − 18a + a2
x2 + h2 = b2 = 81 − 18a + a2
zatem
a2 + 2ax + x2 + h2 = 65
a2 − 2ax + x2 + h2 = 17
−−−−−−−−−−−−−−−−−−−−−−−−−−− dodajemy stronami
2a2 + 2*( x2 + h2) = 82 / : 2
a2 + x2 + h2 = 41
więc po podstawieniu 81 − 18a + a2 za x2 + h2 otrzymamy
a2 + 81 − 18a + a2 = 41
2a2 − 18a + 40 = 0
a2 − 9a + 20 = 0
−−−−−−−−−−−
Δ = 81 − 4*1*20 = 1
| 9 + 1 | ||
a = | = 5 | |
| 2 |
 H = 4 − wysokość graniastosłupa
a , b − długości boków równoległoboku; a > b
h − wysokość równoległoboku
p1 = √33 − długość krótszej przekątnej
p2 = 9 − długość drugiej przekątnej
Mamy
c2 + H2 = 92 = 81
d2 + H2 = (√33)2 = 33
czyli
c2 + 16 = 81 ⇒ c2 = 65
c = √65 ≈ 8,1 − długość dłuższej przekątnej równoległoboku
−−−−−−−−−−−−−
d2 + 16 = 33 ⇒ d2 = 17
d = √17 ≈ 4,1 − długość krótszej przekątnej równoległoboku
−−−−−−−−−−−−−−−−−−−−−
Mamy
( a + x)2 + h2 = c2 = 65
( a − x)2 = h2 = d2 = 17
2a + 2b = 18 ⇒ a + b = 9 ⇒ b = 9 − a ⇒ b2 = 81 − 18a + a2
x2 + h2 = b2 = 81 − 18a + a2
zatem
a2 + 2ax + x2 + h2 = 65
a2 − 2ax + x2 + h2 = 17
−−−−−−−−−−−−−−−−−−−−−−−−−−− dodajemy stronami
2a2 + 2*( x2 + h2) = 82 / : 2
a2 + x2 + h2 = 41
więc po podstawieniu 81 − 18a + a2 za x2 + h2 otrzymamy
a2 + 81 − 18a + a2 = 41
2a2 − 18a + 40 = 0
a2 − 9a + 20 = 0
−−−−−−−−−−−
Δ = 81 − 4*1*20 = 1
H = 4 − wysokość graniastosłupa
a , b − długości boków równoległoboku; a > b
h − wysokość równoległoboku
p1 = √33 − długość krótszej przekątnej
p2 = 9 − długość drugiej przekątnej
Mamy
c2 + H2 = 92 = 81
d2 + H2 = (√33)2 = 33
czyli
c2 + 16 = 81 ⇒ c2 = 65
c = √65 ≈ 8,1 − długość dłuższej przekątnej równoległoboku
−−−−−−−−−−−−−
d2 + 16 = 33 ⇒ d2 = 17
d = √17 ≈ 4,1 − długość krótszej przekątnej równoległoboku
−−−−−−−−−−−−−−−−−−−−−
Mamy
( a + x)2 + h2 = c2 = 65
( a − x)2 = h2 = d2 = 17
2a + 2b = 18 ⇒ a + b = 9 ⇒ b = 9 − a ⇒ b2 = 81 − 18a + a2
x2 + h2 = b2 = 81 − 18a + a2
zatem
a2 + 2ax + x2 + h2 = 65
a2 − 2ax + x2 + h2 = 17
−−−−−−−−−−−−−−−−−−−−−−−−−−− dodajemy stronami
2a2 + 2*( x2 + h2) = 82 / : 2
a2 + x2 + h2 = 41
więc po podstawieniu 81 − 18a + a2 za x2 + h2 otrzymamy
a2 + 81 − 18a + a2 = 41
2a2 − 18a + 40 = 0
a2 − 9a + 20 = 0
−−−−−−−−−−−
Δ = 81 − 4*1*20 = 1
| 9 + 1 | ||
a = | = 5 | |
| 2 |

 ktorego pozdrawiam a zaczyna on
przewaznie tak: ...., no coz i dalej a na koncu zawsze jest
ktorego pozdrawiam a zaczyna on
przewaznie tak: ...., no coz i dalej a na koncu zawsze jest 

