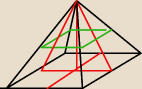
ostosłup ścięty- pomóżcie w sprawdzeniu karmelka: potrzebuję, żeby ktoś sprawdził mi wynik zadanie: W ostrosłupie prawidłowym czworokątnym pole każdej z pięciu ścian równa się1. Ostrosłup ten ścięto w połowie wysokości płaszczyzną równoległą do podstawy. Obliczyć objętość i pole całkowite otrzymanego ostrosłupa ściętego. Zrobiłam to zadanie ale mam prośbę czy mógłby ktoś je rozwiązać i sprawdzić mi wyniki Tak mi wyszło:

	7√13
V=		(j3)
	48

	11
Pc=		(j2)
	4

dobrze czy źle

karmelka: to jak, mógłby ktoś zerknąć na te zadanie?

Mila:

	√15
Ho=
	2

	7√15
V =
	48

	3		1		1
Pc=4*		+1+		=4
	4		4		4

Nie masz odpowiedzi do zadania?

karmelka: niestety nie. to nie są zadania z książek ani zbiorów żadnych. A przynajmniej ja takich nie mam. Sor tłumaczy z obcojęzycznych albo sam wymyśla zadania

Janek191: P_s = 1 P_p = 1 ⇒ a² = 1 ⇒ a = 1 h₁ − wysokość ściany bocznej P_s = 0,5 a*h₁ = 1 ⇒ 0,5*1*h₁ = 1 ⇒ h₁ = 2 h − wysokość ostrosłupa Z tw. Pitagorasa mamy

	3		15
( 0,5 a)2 + h2 = h12 ⇒ 0,25 + h2 = 4 ⇒ h2 = 3,75 = 3		=
	4		4

	√15
h =
	2

V − objętość ostrosłupa

	1		1		√15		√15
V =		Pp*h =		*1*		=
	3		3		2		6

Ostrosłup ścięto w połowie wysokości, więc skala podobieństwa k = 0,5 V₁ − objętość ostrosłupa odciętego Mamy

V1
	= k2 = 0,25
V

	√15
V1 = 0,25*V =
	24

V₂ − objętość ostrosłupa ściętego

	√15		√15		3		√15
V2 = V − V1 =		−		=		√15 =
	6		24		24		8

============================================================= Pole powierzchni całkowitej ostrosłupa ściętego

	1		1		1
Pc = 5 − 4*		+		= 4
	4		4		4

================================

Janek191: Miało być

V1
	= k3
V

Ale wpadka !

Mila: Janku, stosunek objętości brył podobnych jest równy sześcianowi skali podobieństwa.

Janek191:

	1		√15		√15
V1 =		*		=
	8		6		48

więc

	√15		√15		7
V2 = V − V1 =		−		=		√15
	6		48		48

karmelka: ok, liczyłam tak samo, gdzieś w obliczeniach cyferki przekręciłam, za szybko chciałam zrobić Dziękuję