Całki. Elon: Oblicz: ∫|2−x|dx Górne granice całkowania 3 oraz 0.

Elon: Tzn. górna granica 3 a dolna 0... ;X

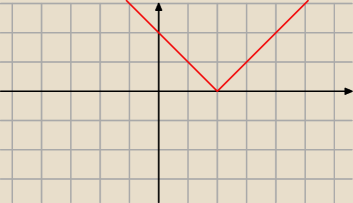
asdf: najlatwiej to sobie rozbic na całkę:

	5
02∫(2−x)dx + 23∫(x−2) dx = ... =		(z rysunku policzylem te pole)
	2

ZKS: Ładnie na rysunku widać te dwa trójkąty.

	1		1		1		5
P = P1 + P2 =		* 2 * 2 +		* 1 * 1 = 2 +		=
	2		2		2		2

Elon: Ja to liczyłem wyznaczając wartość bezwzględną, bez pola (bo nie ogarniam jak to z tym polem się robi...) i wyszło mi takie coś ∫|2−x|dx = ∫(2−x)dx + ∫(x−2) dx= ∫−(2−x)dx + ∫(x−2) dx. Oczywiście granice całkowania przyjąłem jak w podanym przykładzie przez asdf, czyli dolna 0 górna 2 i potem 2 oraz 3.

Elon: ∫|2−x|dx = ∫|2−x|dx + ∫|2−x| dx = ∫−(2−x)dx + ∫(2−x) dx − mała poprawka...

Elon: I teraz jak policzyłem wyszło mi −1... Co zrobiłem nie tak?... Policzyłem całki, podstawiłem z granic...

Elon: TZn. −3 mi wyszło, nie −1... Ale i tak nie powinno tak być... Jak wam wyszły takie wyniki?

Godzio:

	x2		x2		9		5
... = (2x −		)|02 + (−2x +		)|23 = 4 − 2 − 6 +		+ 4 − 2 =
	2		2		2		2

Elon: a skąd to 2x? Czy ∫(2−x)dx to nie jest x−1/2x²

Elon: 1/2*x² − poprawka.

Godzio: Serio ? Proponuję zacząć studia od początku.

Elon: Po prostu nie widzę skąd jest to 2x : / Resztę robię dobrze tutaj, tylko ta jedna rzecz...

asdf: nie wiesz ile to jest ∫2dx

Elon: Cały czas myślałem, że jeśli jest całka z jakiejś liczby to jest x+C...

Elon: OK widzę teraz swój błąd − czyli jak jest całka np z 3 albo 54 to zawsze będzie te 3x albo 54x tak?

asdf: tak, A − stała ∫Adx = A∫dx = A*x + C

Elon: Tzn wiedziałem, że się przerzuca stałą przed całkę... Aaah nie pomyślałem w ogóle, że to właśnie jest tak stała

asdf: zdarza się