Zadanie optymalizacyjne Romeczek : Drut o długości 100 m przecięto w pewnym miejscu i z jednej części zbudowano kwadrat a z drugiej trójkąt równoboczny. W jakim punkcie zgięto, jeżeli suma pól zbudowanych figur jest najmniejsza z możliwych. Zadanie optymalizacyjne.

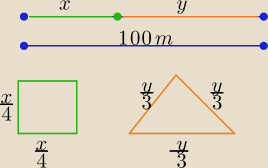
Eta: x>0 , y>0 Z warunku zadania x+y=100 ⇒ x=100−y , y∊(0,100)

	x		1		1		1
P(kwadratu)=(		)2=		x2=		(100−y)2=......= 625−125y+		y2
	4		16		16		16

	1		y		√3
P(tr. równobocznego)=		*(		)2*√3 =		y2
	4		3		36

Suma pól :

	1		√3
P(y)= 625−125y+		y2+		y2 −−− ma mieć minimum( z treści zadania
	16		36

	√3		1
P(y)= (		+		)y2−125y +625 −−− funkcja kwadratowa, wykresem parabola
	36		16

ramionami do góry, zatem funkcja osiąga minimum w wierzchołku paraboli dla odciętej wierzchołka

	−b		125
ymin=		=		= .......
	2a		√3   1   2* +   36   16

	125*18
ymin=
	4√3+9

x_min= 100 −y_min=..... dokończ te nieco..... "koszmarne" rachunki

Saizou : no ale chyba łatwiej oznaczyć 3x oraz 4y, będzie się łatwiej liczyć chyba

Saizou : znaczy się odwrotnie 3y i 4x

Eta: Jak ktoś tak chce

Eta: Zamiast napisać,że ładnie zobrazowałam, to ......... takie uwagi

Saizou : oj tam......... tak na początku pomyślałem że Eta musiała to rozwiązać, bo widać było po formie postu za rysunki itp.

Eta: