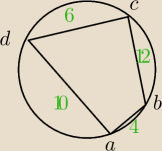
Oblicz pole czworokąta. Mary: Oblicz pole czworokąta. PS. ten czworokąt jest dowolny, to nie jest żadna konkretna figura

Godzio: P = √(p − a)(p − b)(p − c)(p − d) Gdzie p to połowa obwodu. (Wzór Brahmagupty, a po co ten okrąg ? Odpowiedz sobie sam )

Mila: Godzio, uczęszczasz ( w czasie roku akademickiego) na jakieś koło? Bardzo mi się podobają zadania z Uniwersytetu Wrocławskiego. Podziwiam Twoich nauczycieli akademickich za ich aktywność.

Mary: tak nam podał zadanie nauczyciel i niestety tego wzoru nie mieliśmy, więc obawiam się, że to nie przejdzie nie można jakimś innym sposobem tego zrobić?

Godzio: Mila, żebym ja miał jeszcze na to czas, praktycznie całe dnie pracuje Koła są, ale to chyba bardziej dla licealistów, gimnazjalistów.

Godzio: No to trzeba się pomęczyć w takim razie, Prowadzę przekątną AC, korzystam z faktu, że suma kątów na przeciwko jest równa 180^o (wynika to z faktu wpisania czworokąta w okrąg) i lecimy z twierdzenia cosinusów: AC² = 36 + 100 − 2 * 6 * 10 * cosα AC² = 16 + 144 − 2 * 4 * 12 * cos(180 − α) [ cos(180 − α) = − cosα ] Odejmuje równania od siebie:

	1		4√5
0 = 20 − 44 − 120cosα − 96cosα ⇒ cosα = −		⇒ sinα =
	9		9

	1		1
P =		* 6 * 10 * sinα +		* 4 * 10 * sin(180 − α) [ sin(180 − α) = sinα ]
	2		2

Dokończ

Mary: DZIĘKUJĘ!