Funkcja f dana jest wzoremf(x)=x^2-4π x+3π^2 kamczatka: Funkcja f dana jest wzoremf(x)=x²−4π x+3π² a)Znajdź wszystkie liczby całkowite, dla których funkcja f przyjmuje wartości ujemne b)Zapisz wzór funkcji f w postaci iloczynowej c)wyznacz największą i najmniejszą wartość funkcji f osiąganą w przedziale<0,5\pi> Bardzo proszę o rozwiązanie tego zadanka. Z góry niezmiernie dziękuję.

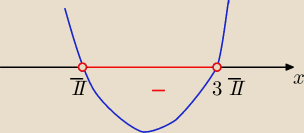
Eta: f(x)=(x−π)(x−3π) −−− postać iloczynowa f(x)<0 ⇔ (x−π)(x−3π)<0 ⇔ x∊(π, 3π) i x∊C ⇒ x={4,5,6,7,8,9} c) nie widzę jaki to przedział ? napisz wyraźniej

Eta:

kamczatka: w c) jest przedział <0;5π>

Eta:

	3π+π
xw=		= 2π ∊<0,5π>
	2

dla y_min= f(2π) = .... f(0)=.... f(5π)= ...... która z nich będzie wartością max ?

kamczatka: jak to postać iloczynowo wyliczyć ? Bo tylko wynik końcowy Eta podała.

Eta: Echhh y= x²−4πx+3π² Δ= 16π²−12π² = 4π² , √Δ= 2π

	4π−2π		4π+2π
x1=		= π v x2=		= 3π
	2		2

y= (x−x₁)(x−x₂)= (x−π)(x−3π)

kamczatka: bo nie byłem pewien czy można Δ obliczać jak współczynnik a jest do ² i c do ²

Eta: a=1 , b= −4π , c=3π² −−−− to są liczby !

kamczatka: a jeszcze mam pytanie f_max będzie f(0) czyli f(0) = 0−0+3π² a w odpowiedziach mam π²

kamczatka: błąd wychodzi 8π²

Eta: f(0)=3π² f(5π)= 25π²−20π²+3π²= 8π² >3π² f(max) = 8π² w przedziale <0, 5π>