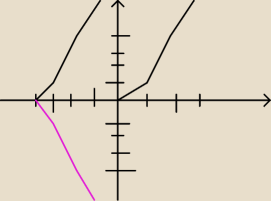
szkicowanie wykresu funkcji Kinia: Naszkicuj wykres funkcji: f(x)=−√x+4 f1(x)=√x−−−−−−−−−>(nad strzałką Tu−>(przekształcenie)[−4,0] (po strzałce tej dużej) f2(x)=√x+4−−−>(nad strzałką s OX)f(x)=−√x+4 Czy dobrze jest to zadanie wykonane? Pierwsza linia u góry po prawej stronie to √x Ta po lewej u góry to przesunięta o przekształcenie, a u dołu − fioletowa, to po odbiciu względem symetralnej OX, jest to dobrze? Pytanie, czy rysunek dobrze wykonałam? Czy przekształcenie powinno być względem symteralnej OX czy jednak OY?(niestety niezbyt wiem czy jednak OX − jeśli dobrze chciałabym by mi ktoś to wyjaśnił) Robiliśmy podobne zadania, ale prostrze... Niezbyt wiem kiedy stosować OX a odbicie OY

sushi_ gg6397228: jest OK symetria wzgledem OX y=f(x) to po symetrii mamy y₁= −f(x)

Kinia: Rysunek również jest dobrze...? Miałam też naszkicować takie dwie funkcje: f(x)=−(x−2)² f1(x)=x² −−−−−>(nad strzałką: Tu[2,0] (za strzałką) f2(x)=(x−2)²−−−>(nad strzałką Sox) f(x)=−(x−2)² f(x)=(2−x)² f1(x)=x² −−−−−>(nad strzałką: Tu[−2,0] (za strzałką) f2(x)=(x+2)²−−−>(nad strzałką Soy) f(x)=(−x+2)² I chciałabym się zapytać, kiedy stosować w takim razie Soy a Sox? I o co chodzi z tym wędrującym minusem w obydwóch przypadkach, bo dla mnie to niezrozumiałe...

sushi_ gg6397228:

sushi_ gg6397228: symetria OY y= f(x) y₁= f(−x)

sushi_ gg6397228: y=−(x−2)² y=x² wyjsciowa potem y₁= (x−2)² −−> przesuwamy o 2 w prawo y₂= −(x−2)² symetria OX

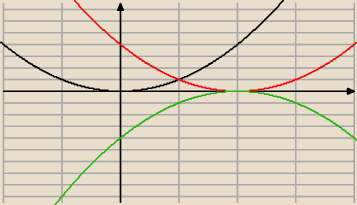
sushi_ gg6397228: czarny−− y=x² zielony y= −(x−2)²

sushi_ gg6397228: robimy przekształcenia, aby lepiej się liczyło y=(2−x)²= [ −(x−2)]²= (x−2)² i teraz wiadomo jak sie za to zabrac

Kinia: Nie rozumiem do końca...

Kinia: ten pierwszy rysunek, dotyczy tego:? f(x)=−(x−2)²2 f1(x)=x² −−−−−>(nad strzałką: Tu[2,0] (za strzałką) f2(x)=(x−2)²−−−>(nad strzałką Sox) f(x)=−(x−2)² Bo w zeszycie mam tu tylko względem oy, nie mam nic poniżej osi x... Nie rozumiem w takim razie co jest źle...?

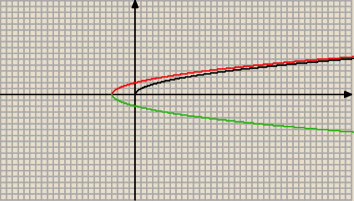
sushi_ gg6397228: o 21.06− wykres pierwiastka−−> zadanie nr 1 poniżej osi OX=== symetria OX na pewno w tym zadaniu jest OX; moze jest bład przy przepisaniu i jest OY

Kinia: Tsaa, już zauważyłam − pomyliłam wartości z argumentami − dziękuję bardzo, rysunek już w zeszycie poprawiam : > Resztę też już chyba zrozumiałam, jeszcze raz wielkie dzięki! =)

sushi_ gg6397228: na zdrowie

Kinia: Tylko... jednak jedno pytanko... Skoro w tym: f(x)=(2−x)² f1(x)=x² −−−−−>(nad strzałką: Tu[−2,0] (za strzałką) f2(x)=(x+2)²−−−>(nad strzałką Soy) f(x)=(−x+2)² na początku jest to (2−x)² co jest tym samym co (x−2)² A później jest (x+2)² po przekształceniu, to nie jest ogólna zmiana −f(x), a nie tylko f(−x)? Nie rozumiem czemu zmienił się w sumie cały zapis, a nie tylko x, a mimo to jest względem osi OY, jak oś OY to f(−x)?

Kinia: Bo jak dla mnie po przekształceniu powinno być − choć wiem że w tej sytuacji nie może (−x+2)², wtedy jest zmiana tylko tego x, a więc odbija się względem osi OY bo f(−x)

sushi_ gg6397228: przeciez nigdzie dalej nie ma y= (x+2)² u mnie

Kinia: Znaczy tfu.... (−x−2)², bo na początku jest (2−x)² czyli (x−2)², a gdy x sie zmieni, bo ma "−" to jest właśnie to f(−x) czyli oy, jak dla mnie (x+2)², to zmiana całego zapisu, a nie tylko argumentu...

Kinia: Mogłabyś pokierować mnie i pokazać błąd w tym: f(x)=(2−x)² f1(x)=x² −−−−−>(nad strzałką: Tu[−2,0] (za strzałką) f2(x)=(x+2)²−−−>(nad strzałką Soy) f(x)=(−x+2)² Po prostu go nie widzę, a mi sie nie zgadza z tym, że jest odbite względem osi OY...

Kinia: Poprosiłabym bardzo...

sushi_ gg6397228: pokazałem jak nalezy zrobić przekształcenie

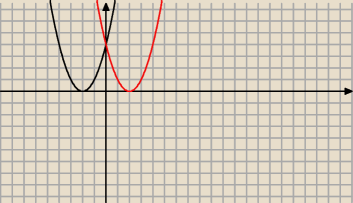
sushi_ gg6397228: w funkcji wyjściowej zrobilem sobie ułatwienie (−x+2)²= (x−2)² i dlatego nie miałem symetrii OY, a przesunięcie o potem symetria OX

sushi_ gg6397228: tamte obliczenia i podobne są "za mocno skomplikowane" i lepiej sobie nie utrudniać

Kinia: Tylko... teraz mówię o tym drugim zadanku, gdzie chyba nie ma odbicia OX Znaczy... Podałam trzy zadanka − jedno na samym początku, a następnie dwa nieco niżej. Teraz mówię o tym drugim z tych dwóch dodanych później. Ten rysunek co wykonałeś to był do tego pierwszego z dwóch zadanek i rozumiem jak najabrdziej, jednakze chodzi mi o drugie zadanko... Gdzie jest przesunięcie a następnie symetria, ale względem OY Nie chodzi mi o zadanko: f(x)=−(x−2)² bo tu będzie OX, bo się po przekształceniu pojawi (x−2)², czyli minus znika, czyli zmiana całej funkcji −> −f(x) A mi chodzi teraz o: f(x)=2−x)²...

sushi_ gg6397228: zrobiłem trik i nie miałem już potem symetrii OY, jak u Ciebie

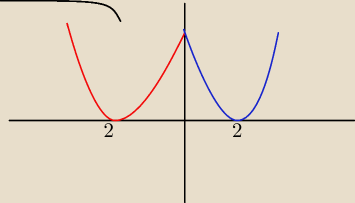
Kinia: f(x)=(2−x)² Najpierw rysuję x² − czarna Później przekształcenie: [−2,0] − czerwona i względem osi OY, gdyż (2−x)² różni się od (x+2)² f(−x) − niebieskie Tak mam zapisane w zeszycie i chciałabym sie zapytać gdzie w takim razie mam bład, albo czy mógłbyś mi wyjasnić czemu jest własnie to OY, a nie OX, skoro jak dla mnie roźni się nie tylko argumentem (f(−x), a całą wartością (−f(x))... Proszę...

Kinia: Czarna jest po środku − ale ją zwiało :c

sushi_ gg6397228: moze na innym przykladzie y=x² OX y₁= −x² y₁= − f(x) OY y₂= (−x)²====x² y₂ = f(−x) wszystko zależy gdzie wstawimy znak minusa, to takie dostaniemy przekształcenie − symetrie i teraz w zadania y= (x+2)² OY y₁= (−x+2)² OX y₂= − (x+2)²

Kinia: Ojej, ojej, ojej − dziękuję prześlicznie! W końcu rozumiem, rozumiem, jeju xd Mi trzeba tłumaczyć czasem jak głupkowi xd Wybacz za czas jaki poświęciłeś, ale wiedz że teraz zasnę spokojnie, jeszcze raz WIELKIE DZIĘKI! =) Spokojnej nocy życzę =)

sushi_ gg6397228: na zdrowie