stosunek objętości kul
karmelka: długość wysokości ostrosłupa prawidłowego trójkątnego jest równa długości krawędzi podstawy.
Oblicz stosunek objętości kuli wpisanej w ten ostrosłup do objętości kuli opisanej na nim.
Proszę o pomoc, albo jakieś wskazówki do rozwiązania, bardzo mi to potrzebne

4 wrz 18:23
irena_1:
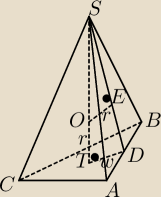
|ST|=|AB|=a
|OS|=a−r
|SD|=h
| | 3 | | 39 | |
h2=a2+w2=a2+ |
| a2= |
| a2 |
| | 36 | | 36 | |
r
√13=a−r
r(
√13+1)=a
r− promień kuli wpisanej w ostrosłup
4 wrz 18:50
irena_1:
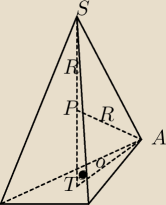
|ST|=a
|PT|=a−R
(a−R)
2+o
2=R
2
a
2−2aR+R
2+o
2=R
2
| | 3 | | 12 | | 4 | |
2aR=a2+ |
| a2= |
| a2= |
| a2 |
| | 9 | | 9 | | 3 | |
R− promień kuli opisanej na ostrosłupie
4 wrz 18:54
irena_1:
| Vw | | r | | √13−1 | | 13√13−39+3√13−1 | |
| =( |
| )3=( |
| )3= |
| = |
| Vo | | R | | 8 | | 512 | |
| | 16√13−40 | | 2√13−5 | |
= |
| = |
| |
| | 512 | | 64 | |
4 wrz 18:56
karmelka: Super

dziękuję ślicznie za pomoc

4 wrz 20:31

 |ST|=|AB|=a
|OS|=a−r
|ST|=|AB|=a
|OS|=a−r
 |ST|=a
|PT|=a−R
|ST|=a
|PT|=a−R
 dziękuję ślicznie za pomoc
dziękuję ślicznie za pomoc 