geometria zadanie: 1. Czy dowolne dwie figury z podanego zbioru sa przystajace a) zbiór wszystkich kwadratów o boku długosci 7 ; b) zbiór wszystkich prostokatów o przekatnej długosci 7 ; c) zbiór wszystkich rombów o boku długosci 7 ; d) zbiór wszystkich trójkatów prostokatnych równoramiennych o przeciwprostokatnej długosci 7 ? wedlug mnie: a) TAK b) TAK c) NIE d) TAK ale w odp. jest w b) NIE moglbym prosic o wytlumaczenie dlaczego? a jezeli mozna to do d) tez mimo, ze mialem dobrze

Janek191: a) Tak b) Nie c) Nie d) Tak Ad . b) Np. Kwadrat o przekątnej o długości 7 i prostokąt nie będący kwadratem o przekątnej o długości równej 7 nie są figurami podobnymi. Ad. d) Te trójkąty mają identyczny kształt.

zadanie: ok dziekuje

zadanie: no tak bo kazdy kwadrat jest prostokatem i wtedy wyjdzie kwadrat(prostokat) i prostokat czyli nie beda przystajace nie naloza sie na siebie

Mila: d) kształt i wielkość.

zadanie: 2. Czy w trójkacie o bokach podanej długosci kazdy z trzech katów ma miare mniejsza od 120^o a) 2, 3, 4 odp, tak 3. Czy w trójkacie o bokach podanej długosci istnieje kat majacy miare mniejsza od 60^o a) 2, 3, 4 odp. tak probowalem korzystac z twierdzenia Cosinusow a sa jakies szybsze sposoby?

zadanie: wyszlo mi, ze 2 katy sa ostre czyli mniejsze od 120^o i jeden jest rozwarty bo wyszedl ujemny ale nie wiadomo czy mniejszy od 120⁰. wiec obliczylem przyblizona wartosc tego kata i na postawie wykresu funkcji cosinus uznalem, ze ten kat jest mniejszy od 120^o a mozna inaczej?

zadanie: zalezaloby mi jeszcze na zadaniu 2 i 3

Mila: 3) zacznij od obliczenia cosinusa kąta leżącego naprzeciw boku 2. To będzie cosinus najmniejszego kąta (wiesz dlaczego?)

Mila: 2) oblicz cos120 oblicz cosinus kata leżącego naprzeciw boku 4. cosinus jest funkcją malejącą w przedziale (0,π), porównaj wartości cos 120 i cos α i wyciągaj wnioski co do argumentów.

zadanie: 3) a=2, b=3, c=4

	7
cosα=		=0,875
	8

najmniejszego kata bo naprzeciw najmniejszego boku znajduje sie najmniejszy kat

zadanie:

	1
2) cos120o=cos(90o+30o)=−sin30o=−
	2

	1
cosγ=−		=−0,25
	4

	7
cosα=		=0.875
	8

zadanie:

	11
cosβ=		≈0,68
	16

Mila: porównujesz cos γ>cos120⇔γ<120 odp. Tak

zadanie: 3) cos60^o=0,5 czyli cosα i cosβ < 60^o bo maja wieksze wartosci bo ta funkcja jest malejaca w podanym przedziale czyli odp. tak

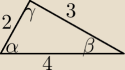
Mila: 2²=3²+4²−2*3*4 *cosβ 4=9+16−24 cos β 4−25=−24 cosβ

	21		7		1
cosβ=		=		>		⇔cosβ> cos 60⇔β<60
	24		8		2

najmniejszy kąt tego Δ jest mniejszy od 60. odp. tak

Mila: 23:17 nie możesz pisać: cosβ < 60^o to błąd.

zadanie: czyli poprawnie β<60^o

zadanie: a ja chyba zle oznaczylem te boki bo u mnie naprzeciwko boku o dlugosci 2 byl kat α czy to nie ma znaczenia?

Mila: Nie ma znaczenia, byle konsekwentnie .

zadanie: dziekuje