zadanie ICSP: Wyznaczyć ekstrema lokalne funkcji : f(x) = x * √4 − x²

ZKS: To zadanie jest dla kogoś?

ICSP: dla wszystkich Nie wiem jak je zrobić

ZKS: D_f = [−2 ; 2]

	x2
f'(x) = √4 − x2 −
	√4 − x2

D_f' = (−2 ; 2) f'(x) = 0 ⇒ 4 − x² − x² = 0 ⇒ x = ±√2 W otoczeniu punktu x = −√2 pierwsza pochodna zmienia znak z − na + więc mamy minimum w otoczeniu punktu x = √2 pierwsza pochodna zmienia znak z + na − więc mamy maksimum.

ICSP: a x = 2 oraz x = −2 ? Nie są zawarte w dziedzinie pochodnej

PW: Rozumiem, że zadajesz zagadkę, którą trzeba rozwiązać bez stosowania zbędnego skomplikowanego aparatu matematycznego.

ZKS: Niestety nie ponieważ mamy ułamek.

ZKS: Właśnie pewnie chodzi o to żeby zrobić bez stosowania pochodnej.

ICSP: Po prostu chce wiedzieć co zrobić kiedy dziedzina funkcji jest większa od dziedziny pochodnej

asdf: czesc wspolna

PW: Na kkrańcach liczyć f(−2) i f(2) i wyciągać wnioski (to też mogą być punkty, w których funkcja osiąga ekstremum lokalne).

Basia: 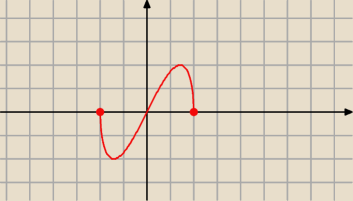Definicja Funkcja f(x), przyjmuje w punkcie x₀, maksimum lokalne (odpowiednio: minimum lokalne), jeśli w pewnym otwartym otoczeniu tego punktu (np. w pewnym przedziale otwartym) funkcja nigdzie nie ma wartości większych (odpowiednio: mniejszych). 1. O jakim otwartym otoczeniu można mówić jeżeli mamy do czynienia z końcami przedziału, w którym funkcja jest określona ? Pamiętajcie, że punkt musi należeć do tego otoczenia. 2. Warunek konieczny istnienia ekstremum lokalnego w p−cie x₀: funkcja f(x), musi być dwukrotnie różniczkowalna w pewnym otoczeniu punktu x₀, f'(x₀)=0 i f"(x) jest w punkcie x₀ ciągła Na końcach przedziału nie ma i być nie może ekstremów lokalnych.

PW: Mówimy, że funkcja f:A→R (A⊂R) ma maksimum lokalne w punkcie x₀∊A, jeśli istnieje takie otoczenie V punktu x₀, że f(x)≤f(x₀) dla każdego x∊V∩A. Zmieniając zwrot nierówności ≤ na przeciwny otrzymuje się definicję minimum lokalnego. Jest to cytat z książki Andrfzej Birkholc, Analiza matematyczna dla nauczycieli, PWN, Warszawa 1977. Ja nie wymyślam definicji. Na zdrowy rozum − a czymże jest f(2)=0 w tym przykładzie, jak nie minimum funkcji na pewnym kawałku dziedziny?

Basia: otoczenie punktu x₀ = zbiór otwarty U taki, że x₀∊U

Basia: P.S. cytowałam Fichtenholtza

PW: Dobrze, ja nie dyskutuję z tym co to jest otoczenie, jeno zwracam uwagę, że w definicji ekstremum lokalnego jest ten kruczek zaznaczony na czerwono (bierzemy iksy z tej części otoczenia, która mieści się w dziedzinie). Dzięki temu można np. mówić o ekstremum lokalnym dla funkcji o "rzadkiej" dziedzinie, czy o przypadku występującym w zadaniu ICSP.

Mila: Wg Krysickiego na krańcach nie określa się ekstremów. Może być wartość najmniejsza ( największa) w jakimś przedziale.

ICSP: Czyli w pkt x = ± 2 funkcja nie ma ekstremów Dziękuję bardzo

Mila: ICSP, jednak poszukaj w literaturce. Trzeba wziąć pod uwagę, to co pisze PW. Panta rhei.

Bogdan: "dziedzina funkcji jest większa od dziedziny pochodnej" − to sformułowanie nie jest prawdziwe, to są zbiory liczbowe, każdy zawiera nieskończenie wiele liczb; można co najwyżej stwierdzić, że jeden zbiór zawiera się w drugim.

PW: Bogdanie, a jakiej Ty definicji ekstremum lokalnego się uczyłeś? Czasami okazuje się, jak trudne bywają proste pytania, i jak pamięć jest zawodna. Ja twierdzę z całą powagą, że funkcja narysowana przez Basię ma minima lokalne w −2 i 2.

Vizer: Dla mnie ciekawym przykładem jest zbadanie ekstremum funkcji np. takiej f(x) = (x + 1)³√(2 − x)². Po zerowaniu pochodnej nie wychodzi nic ciekawego, a okazuje się, że ekstremum jest w x = 2. Nawet wolfram nie określił tego ekstremum, mimo, że na wykresie widać, że jak najbardziej jest. Tak samo f(x) = x² dla x ≠ 0, wydaje mi się, że nie ma ekstremum w x = 0, bo nie należy do ustalonej dziedziny, natomiast wolfram wypisuje, że istnieje. Wniosek : wolfram całej prawdy nam nie powie. Polecam sobie zrobić tą pierwszą funkcję co podałem, niby zagadnienie ekstremów wydaje się nietrudne i tematem oklepanym, ale czasem jest coś w stanie zaskoczyć

Saizou : zacne grono tutaj się zebrało powiem, że geogebra pokazuje: minimum (−√2:−2) maximum (√2:2)

Vizer: Eh tam pomyliłem się w przepisywaniu powinno być f(x) = (x + 1) ³√(2 − x)²

Bogdan: Przepraszam PW, że od razu nie odpowiedziałem. Nie wypowiedziałam się w sprawie ekstremum, a w sprawie sformułowania dotyczącego zbiorów poza kontekstem zadania tu omawianego. Uważam, że w przypadku dwóch zbiorów liczbowych A i B o nieskończonej liczbie liczb nie można użyć sformułowania "zbiór A jest większy od zbioru B", można natomiast powiedzieć, że np. A⊂B.

Bogdan: Jeśli chodzi o ekstremum funkcji, to przychylam się do opinii Basi. Podam znaną mi definicję otoczenia punktu. Otoczeniem o promieniu r punktu P₀ płaszczyzny lub przestrzeni nazywamy zbiór O(P₀; r) := {P : |P₀P| < r} (czyli otwarte koło na płaszczyźnie i otwartą kulę w przestrzeni). Inne określenie. Otoczenie punktu – w topologii oznacza dowolny zbiór, który zawiera zbiór otwarty zawierający dany punkt. Pytanie odnośnie rozpatrywanego zadania − czy punkty (−2, 0) i (2, 0), o których PW mówi, że w nich są ekstrema, należą do jakiegoś zbioru otwartego?