Geometria analityczna - obraz punktu fragresist: Wyznacz obraz punktu P=(2,3) w symetrii względem prostej x+2y=0

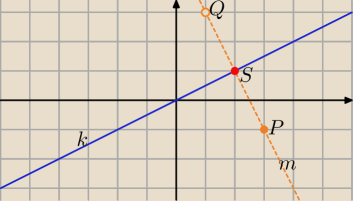
Bogdan: prosta k: y = ax + b, punkt P = (x_P, y_P), obraz punktu P w symetrii względem prostej k

	−1
Q = (xQ, yQ), prosta m⊥k przechodząca przez punkt P: y =		(x − xP) + yP,
	a

punkt S = (x_S, y_S) jest środkiem odcinka PQ

	−1
Po rozwiązaniu układu równań: y = ax + b i y =		(x − xP) + yP otrzymamy xS, yS.
	a

x_Q = 2x_S − x_A i y_Q = 2y_S − y_Q

pigor: ..., niech P'=(x,y)= ? − szukany obraz punktu P, to kolejno np. tak : 1) 2(x−2)−1(y−3)=0 ⇔ 2x−y−1=0 − równanie prostej przez P prostopadłej do danej, 2) y=2x−1 i x+4x−2=0 ⇔ x=0,4 i y= −0,2 , czyli S=(0.4,−0.2) − punkt przecięcia się tych prostych , 3) ze wzoru na środek odcinka − tu PP' : x+2= 0,8 i y+3= −0,4 ⇔ ⇔ (x,y)= (−1.2,−3,4)= (−⁶₅,−¹⁷₅) P' − szukany obraz punktu P. ...

fragresist: a co to jest za równanie x+4x−2=0?

fragresist: dobra, już wiem, wielkie dzięki

PW: Można też podejść do tego tak jak przy wyznaczaniu obrazu symetrycznego za pomocą cyrkla. Napisać równania dwóch dowolnych okręgów o środkach na prostej x+2y=0 zawierających punkt P. Punkty na prostej dobrać inteligentnie, żeby równania okręgów nie były zbyt skomplikowane. Rozwiązać układ równań (równania tych okręgów), który pokaże szukany punkt symetryczny (jednym rozwiązaniem układy będą oczywiście współrzędne punktu P, my szukamy tego drugiego).