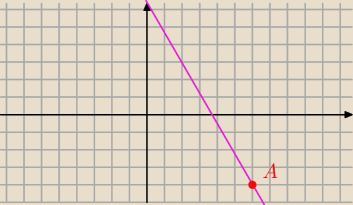
prosta przechodząca przez punkt trrrn: wyznacz równanie prostej przechodzącej przez punkt A (6,−4) i przecinającej oś OX pod kątem 120 stopni

bezendu: tg120⁰=−√3 y=−√3x+b −√3*6+b=−4 −3√6+b=−4 b=−4+6√3 y=−√3x−4+6√3

Bogdan: od razu korzystając z y = a(x − x₀) + y₀: y = −√3(x − 6) − 4 ⇒ y = −√3x + 6√3 − 4

pigor: ..., np. z równania prostej przez 1 punkt (x_o,y_o) : y−y_o = a(x−x_o) mamy y+4 = a(x−6) , gdzie a=tg120^o= tg(180^o−60^o)= −tg60^o= −√3, czyli y=√3(x−6)−4 − szukane równanie prostej . ... :

pigor: ..., przepraszam "zgubiłem'' znak − przy √3