Twierdzenie Talesa Pani: W trójkącie ABC wysokość CD dzieli bok AB na odcinki długości AD=4 cm i DB=10 cm. Bok BC ma dł. 16 cm. Wyznacz długości odcinków, na jakie symetralna boku AB podzili bok BC.

AROB: pomagam

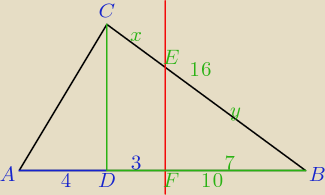
AROB: Szukane odcinki: x i y, y = 16 − x Symetralna EF∥ CD , więc z tw. Talesa prawdziwa jest np. proporcja:

	IFBI		IDFI
		=
	IBCI		ICEI

	10		3		3 * 16
		=		⇒ x =		= 4,8
	16		x		10

y = 16 − 4,8 = 11,2

Pani: dzięki wielkie

xyz: W proporcji zamiast |FB| powinno być chyba |DB| odcinek 10cm równa się odcinek |DB|

Kajak: β kartka

Kasia: punkt c d dzielą odcinek a b c o długośći 27cm na trzy odcinki których stosunek długości jest równy 5:3:1 .Jaka jest długość każdego z tych odcinków

5-latek : czesc prostej ograniczonej z dwoch stron punktami (wzieta z tymi punktami ) nazywamy odcinkiem . Wobec tego poraw tresc zadania bo nie moze byc odcinek ABC I z tego co jeszcze pamietam to punkty na plaszczyznie oznacza sie duzymi literami .czyli A,B D F itd

pigor: ..., no cóż, jakiś nawiedzony(a) N−l (ka) uważa, że tak też może być (mieli zapewne na myśli długości) i dyktował(a) ... z głowy, no to jest dobrze, jest dobrze no i ... dobrze, a więc z warunków zadania jeśli a+b+c= 27 ⇒ 5x+3k+k=27 i k∊R₊ ⇒ 9k=27 ⇔ k=3 , więc a= 5k= 5*3= 15 i b= 3k= 3*3= 9 i c= k= 3 , czyli (a,b,c)= (15,9,3) . ...