liczby zespolone Asia: Hej Mam problem z zadaniem z liczb zespolonych. [iz²+(2−3i)z+⁵₂i]*(z−sprzężenie z+ 5) =0 wiem, że pierwszą część robię jak równanie kwadratowe, ale druga już mi nie wychodzi ;[

ICSP: jeżeli z = x+yi to ile będzie wynosiło z − ź gdzie ź oznacza sprzężenie ?

ICSP: warto zaznaczyć ze zarówno x jak i y muszą być liczbami RZECZYWISTYMI

Asia: x+iy−x−iy czyli zero, ale przepraszam − wkradła mi się literówka − powinno być '5i' i właśnie nie wiem co z tym 5i=0 zrobić, skoro muszę też zapisać wyniki z tej cześci równania...

ICSP: Gdy z = x + yi to ź = x − yi dla x,y ∊R z − ź = x + yi − (x − yi) = ....

Asia: =2iy 2iy+5i = 0 i(2y+5) =0 czyli wtedy y=−3 i x=0

ICSP: x ∊R oraz y = −2,5 czyli to równanie spełniają wszystkie liczby zespolone których cześć urojona jest równa − 2,5

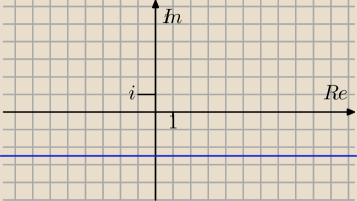
ICSP: Oraz interpretacja tych liczb na płaszczyźnie

Asia: Chyba jednak nie rozumiem rozwiązania... ;[

ICSP: której części dokładnie ?

Asia: czy mogę napisać x=0 zamiast x należy do R? i czy jeśli tak, to jakby y=0 też mam inny zapis?

ICSP: tutaj nie ma żadnego innego zapisu . Rozwiązujemy równanie : z − ź + 5i = 0 ⇒ z − ź = −5i Przyjmując z = x + yi gdzie x,y ∊R mamy : x + yi − x + yi = −5i 2yi = −5i y = −2,5 − to jest rozwiązanie równania. Jak widać nie mamy tutaj x wiec możemy go sobie wybrać dowolnie z liczb rzeczywistych. Weźmy x = 5 5 −2,5i − 5 − 2,5i = −5i a teraz zostawmy po prostu x x − 2,5i − x − 2,5i = −5i Nie ma znaczenia co wstawię za x. Na samym początku rozwiązywania równania i tak się łądnie skróci.

Asia: O, dziękuję bardzo, teraz wszystko jasne