pole obszaru oznaczonego geniusz: 3.oblicz pole obszaru oznaczonego krzywymi o równaniach x²+y+2x−3 = 0 oraz x−y+3=0

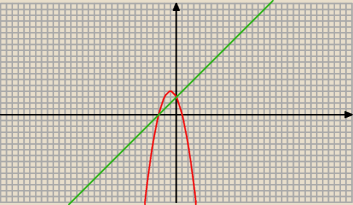
Janek191: x² + y + 2x − 3 = 0 x − y + 3 = 0 można zapisać y = − x² − 2 x + 3 y = x + 3 zatem − x² − 2x + 3 = x + 3 x² + 3x = 0 x*( x + 3) = 0 x₁ = − 3 x₂ = 0 Pole ograniczone parabolą i prostą jest równe 0 0 0 P = ∫ ( − x² − 2x + 3) dx − ∫ ( x + 3) dx = ∫ [ ( − x² − 2x + 3) − ( x + 3)] dx = −3 −3 − 3 0 0

	1		3		27
= ∫ ( − x2 − 3 x ) dx = [ −		x3 −		x2 ] = 0 − [ 9 −		] =
	3		2		2

− 3 − 3 = − ( 9 − 13,5) = 4,5 ================

geniusz: skad sie to wzieło ? x² + 3x = 0

Kuba:

geniusz: ?

pigor: ..., lewą stronę"przeniósł" na prawą i zredukowł, czyli − x² − 2x + 3 = x + 3 ⇔ 0= x²+2x−3+x+3 ⇔ 0= x²+3x ⇔ x²+3x= 0 i tyle . ...

geniusz: o fajnie bo nie mogłem dojść do tego dziekuje