wyl. monotoniczności 67543: Wylicz monotoniczność funkcji √x + 1 w przedziale (2;∞)

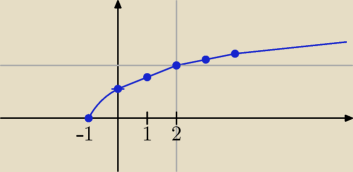
Bogdan: Rysunek przedstawia szkic wykresy funkcji. Monotoniczności się nie wylicza, monotoniczność się wyznacza. f(x) = √x + 1 Założenie: x + 1 ≥ 0 ⇒ x ≥ −1. Dziedzina D_f: x ∊ <−1, +∞) Funkcja f(x) = √x + 1 jest rosnąca w całej dziedzinie, a więc także dla x∊(2 +∞). Sformułuj porządnie treść polecenia w tym zadaniu.

Bogdan: Treść zadania powinna być taka: określ monotoniczność funkcji f(x) = √x + 1. Dziedzina D_f: x ∊ <−1, +∞) Założenie: x₂ − x₁ > 0 i x₁ ≥ −1 i x₂ ≥ − 1 Badamy znak różnicy: f(x₂) − f(x₁). f(x₂) − f(x₁) = √x₂ + 1 − √x₁ + 1 =

	( √x2 + 1 − √x1 + 1 )*( √x2 + 1 + √x1 + 1 )
=		=
	√x2 + 1 + √x1 + 1

	x2 + 1 − x1 − 1		x2 − x1
=		=		> 0
	√x2 + 1 + √x1 + 1		√x2 + 1 + √x1 + 1

ponieważ x₂ − x₁ > 0 z założenia i √x₂ + 1 + √x₁ + 1} > 0 dla x₁, x₂ ≥ −1. Jeśli f(x₂) − f(x₁) > 0 to funkcja f(x) jest rosnąca w całej dziedzinie.