


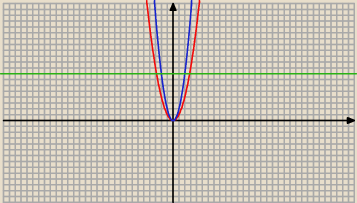
 y = x2
y =2 x2
y = 8
więc
x2 = 8 ⇒ x = − √8 = − 2√2 lub x = 2√2
oraz
2 x2 = 8 ⇒ x2 = 4 ⇒ x = − 2 lub x = 2
Ze względu na symetryczność wykresu mamy
P = 2*P1
2 2√2 2√2 2 2√2 2√2
P1 = ∫ 2 x2 dx + ∫8 dx − ∫ x2 dx = 2 ∫ x2 dx + 8 ∫ dx − ∫ x2 dx
0 2 0 0 2 0
y = x2
y =2 x2
y = 8
więc
x2 = 8 ⇒ x = − √8 = − 2√2 lub x = 2√2
oraz
2 x2 = 8 ⇒ x2 = 4 ⇒ x = − 2 lub x = 2
Ze względu na symetryczność wykresu mamy
P = 2*P1
2 2√2 2√2 2 2√2 2√2
P1 = ∫ 2 x2 dx + ∫8 dx − ∫ x2 dx = 2 ∫ x2 dx + 8 ∫ dx − ∫ x2 dx
0 2 0 0 2 0
 y = x2
y =2 x2
y = 8
więc
x2 = 8 ⇒ x = − √8 = − 2√2 lub x = 2√2
oraz
2 x2 = 8 ⇒ x2 = 4 ⇒ x = − 2 lub x = 2
Ze względu na symetryczność wykresu mamy
P = 2*P1
2 2√2 2√2 2 2√2 2√2
P1 = ∫ 2 x2 dx + ∫8 dx − ∫ x2 dx = 2 ∫ x2 dx + 8 ∫ dx − ∫ x2 dx
0 2 0 0 2 0
y = x2
y =2 x2
y = 8
więc
x2 = 8 ⇒ x = − √8 = − 2√2 lub x = 2√2
oraz
2 x2 = 8 ⇒ x2 = 4 ⇒ x = − 2 lub x = 2
Ze względu na symetryczność wykresu mamy
P = 2*P1
2 2√2 2√2 2 2√2 2√2
P1 = ∫ 2 x2 dx + ∫8 dx − ∫ x2 dx = 2 ∫ x2 dx + 8 ∫ dx − ∫ x2 dx
0 2 0 0 2 0
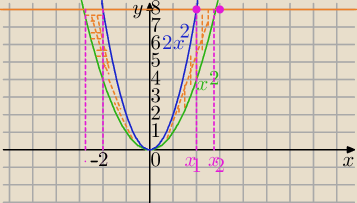 Granice całkowania :
x2=8
x=√8 lub x=−√8
x=2√2 lub x=−2√2
2x2=8
x=2 lub x=−2
P=−2√2∫2√2 (8−x2)dx−−2∫2(8−2x2}dx=
Granice całkowania :
x2=8
x=√8 lub x=−√8
x=2√2 lub x=−2√2
2x2=8
x=2 lub x=−2
P=−2√2∫2√2 (8−x2)dx−−2∫2(8−2x2}dx=
| 64√2+64 | ||
P= | ||
| 3 |



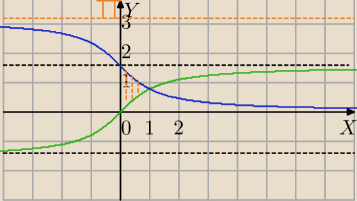 y=arctg(x),
y=arcctg(x)
Punkt przecięcia:
arctgx=arcctgx⇔
y=arctg(x),
y=arcctg(x)
Punkt przecięcia:
arctgx=arcctgx⇔
| π | ||
arctgx= | −arcctgx⇔ | |
| 2 |
| π | |
−arcctgx=arcctgx⇔ | |
| 2 |
| 1 | ||
arcctgx= | π | |
| 4 |