Jak rozwiązać równanie trygonometryczne z wartością bezwzględną.
Svart: Rozwiąż równanie.
sin(x/2) = 1 + |sin(x)|
Jak rozwiązywać takie zadania? Wrzuciłem tu najłatwiejszy z przykładów, które muszę zrobić.
Najtrudniejszy prawdopodobnie będzie: (x−2)2 |cos(x)| = cos(x)
W rozwiązaniach nie wolno mi użyć wzoru na Δ.
1 wrz 00:24
AS: Rozpatrz trzy przypadki:
sin(x) > 0 wtedy |sin(x)| = sin(x)
sin(x) = 0 wtedy |sin(x)| = 0
sin(x) < 0 wtedy |sin(x)| = −sin(x)
do rozwiązania trzy proste równania trygonometryczne.
Pamiętaj o założeniach.
1 wrz 09:00
pigor: ... , np. tak :
(x−2)2 |cos(x)| = cos(x) ⇔
⇔ [cos(x) ≥0 i (x−2)
2cos(x)− cos(x)= 0] lub [cos(x)< 0 i cos(x)+(x−2)
2cos(x)=0] ⇔
⇔ [cos(x) ≥0 i cos(x)*((x−2)
2−1)= 0] lub [cos(x)< 0 i cos(x)*(1+(x−2)
2)=0] ⇔
⇔ [cos(x) ≥0 i (cos(x)=0 lub |x−2|=1] lub x∊∅ ⇔
⇔ cos(x)= 0 lub (cosx ≥0 i x−2=±1) ⇔
⇔ x=
12π+2kπ lub [0≤ cosx ≤1 i (x=3 lub x=1)] ⇔
⇔
x=12π+2kπ, gdzie k∊Z, lub
x=1 . ...

1 wrz 13:14
Svart: AS: To się nie sprawdzi.
| | 1 | | 1 | |
pigor: Dało się łatwiej i popełniłeś błąd. nie |
| π+2kπ tylko |
| π+kπ. |
| | 2 | | 2 | |
Natomiast ten pierwszy przykład okazał się podpuchą, wystarczy porównać zb. wartości strony
lewej i prawej a ma się rozwiązanie na dłoni.
1 wrz 22:14
mars:
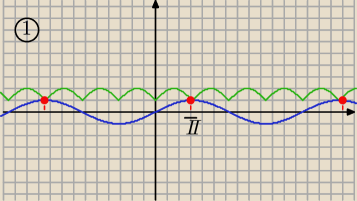
1 wrz 22:25
Svart: No nie mówię, że nie ma rozwiązań, chodziło mi o to, że jeśli porówna się zb. wartości to od
| | x | |
razu widać, że cos |
| =1 i cos(x)=0 |
| | 2 | |
1 wrz 22:37
Svart: | | x | |
lub cos |
| =0 i cos(x)=−1 |
| | 2 | |
1 wrz 22:41
Svart: Ups... Teraz to walnąłem głupotę, bez tego "lub"
1 wrz 22:47

