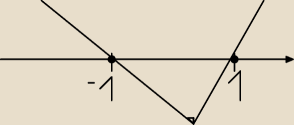
Wyrażenia algebraiczne Kamix: Gdzie popełniam błąd? Niby prosta nierówność, a wynik nie zgadza się z odpowiedzią.... Jestem pewny, że to przez źle narysowany wykres, zasady znam, a nie wiem gdzie robię błąd / −x³+x²+x−1≥0 No to do dzieła: x²(−x+1)−1(−x+1)≥0 (x²−1)(−x+1)≥0 (x+1)(x−1)(−x+1)≥0 x+1=0⋁x−1=0⋁−x+1=0 x=−1⋁x=1⋁x=1 No i teraz wykres: Mamy dwa miejsca zerowe, a więc wykresem będzie parabola. Zaczynam od góry, gdyż mam x². A więc, x∊(−∞;−1>∪<1;+∞) W odpowiedzi mam, że x∊(−∞;−1>∪{1}. Wytłumaczcie mi gdzie popełniam błąd...

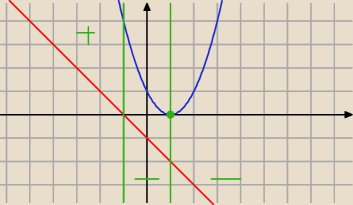
Basia: 1. wykresem nie jest parabola bo masz wielomian 3 stopnia 2. (x+1)(x−1)(−x+1) = (x+1)(x−1)[−(x−1)] = −(x+1)(x−1)² 3. teraz rysujesz y = −(x+1) = −x−1 i y = (x−1)² 4. mamy (−∞;−1>∪{1}

Kamix: Basiu, bardzo dziękuję ; )

Kamix: A można to rozwiązać w bardziej szablonowy sposób, wykorzystując oś i pierwiastki wielomianów, że parzystokrotny odbija, nieparzystokrotny przebija oś i wtedy odczytać? Bo w Twojej skutecznej metodzie, trzeba rysować proste, a tam tylko zwracać uwagę na to, czy pierwiastek jest parzystokrotny czy nie i rysować?

Kamix: Okey, zauważyłem już, że z powodzeniem można, wynik wyszedł identyczny.

PW: (x+1)(x−1)(−x+1)≥0 Tu trzeba przekształcić do postaci (x+1)(x−1)²≤0 i dopiero rysować "mechanicznie", tak jak jesteś przyzwyczajony

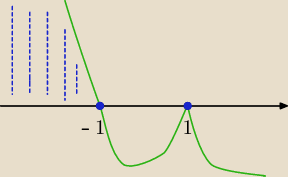
Saizou : oczywiście że można rozwiązać to w "szablonowy" sposób otrzymaliśmy pierwiastki x₁=−1 x₂=1 x₃=1 (x₂=x₃ zatem jest to parzystokrotny pierwiastek ) i nasz wielomian 'zaczynał się' od współczynnika ujemnego, zatem rysujemy 'wężyka' od dołu do prawej strony i doczytujemy kiedy wykres jest nad lun na osi x x∊(−∞:−1>∪{1}