Pochodne - potrzebna pomoc Łukasz: Obliczyć I−szą pochodną funkcji jednej zmiennej:

	1−cos x
a) f(x)=
	sin x

b) f(x)=exp ln √x−1 Narysować krzywe i obliczyć pole obszaru płaskiego ograniczonego przez te krzywe : y=x² oraz y=2x

	1
Wyznaczyć ekstremum oraz przedziały monotoniczności funkcji określonej wzorem : y=x2 e
	x

	1
(		to potęga e)
	x

Łukasz: Osobe ktora to rozwiąże prosze o pozostawienie kontaktu do siebie (mail, skype) ponieważ ja i paru moich znajomych z chęcią weźmie korki online (oczywiście odpłatne) z zakresu pochodnych i całek.

Janek191:

	1 − cos x
a) f(x) =		; x ≠ k*π gdzie k jest liczbą całkowitą
	sin x

Korzystamy z wzoru na pochodną ilorazu funkcji :

	f		f '*g − f* g'
(		) ' =
	g		g2

zatem

	sin x * sin x − ( 1 − cos x)*cos x
f ' (x) =		=
	sin2 x

	sin2 x − cos x + cos2 x		1 − cos x
=		=
	sin2 x		sin2 x

bo sin² x + cos ² x = 1 b) f(x) = e^{ln √x −1} ; x > 1 Korzystamy z wzoru na pochodną funkcji złożonej f '(x) = e^{ln √ x − 1}*( ln √x −1) ' * ( √x −1) ' * ( x − 1) ' =

	1		1		1
= e ln √ x − 1 *		*		*1 = 0,5*eln √x −1*		=
	√x−1		2 √x−1		x −1

	0,5 e ln √x −1
=
	x − 1

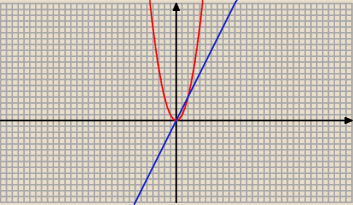Janek191: y = x² y = 2 x x² = 2x x² −2x = 0 x*( x − 2) = 0 x₁ = 0 x₂ = 2 zatem pole 2 2 2 2

	1
P = ∫ 2x dx − ∫ x2 dx = ∫ ( 2 x − x2 ) dx = [ x2 −		x3 ] =
	3

0 0 0 0

	1		8		4
= 22 −		*23 = 4 −		=
	3		3		3