Pole figury Jakub: Oblicz pole figury ograniczonej o danych równaniach: y=x²− 2x x² −2x + y²=0 Wyszła mi parabola o miejscach zerowych '0' i '2' oraz okrąg o środku (1,0) i promieniu 1. (x−1)² + y² = 1 I chciałbym się zapytać jak policzyć teraz pole?

wredulus_pospolitus: całki mieliśmy

Jakub: Tak. Ale nie wiem jak zapisać tutaj te ograniczenia z góry i dołu

Jakub: Chyba że... ∫(x²−2x+y²)−(x²−2x) Z dołu 0 i z góry 2?

wredulus_pospolitus: jaki wzór ma funkcja określająca górne półkole <−−− pierwsza funkcja parabola <−−− druga funkcja a całka jest od 0 do 2

Jakub: Czyli pierwszą całkę która zapisałem wyżej /2 ?

wredulus_pospolitus: niii −y²=x²−2x y² = 2x−x² y = √2x−x² <−−− górne półkole y = −√2x−x² <−−− dolne półkole interesuje Ciebie górne

wredulus_pospolitus: albo prościej jeszcze ... patrzysz jakie jest pole paraboli poniżej połowy okręgu ... i dodajesz do tego polowe pola okręgu (wyliczonego ze wzoru )

Jakub: ∫√2x−x² − (x²−2x) dx Tak?

wredulus_pospolitus: si

Jakub: A to co prościej, bo chyba nie za bardzo zrozumiałem Czyli, że ta parabola jest z góry ograniczona x=0 a z dołu (x²−2x) Dobrze zinterpretowałem? No i dziękuje za pomoc

Jakub: wredulus_pospolitus: a jak mam coś takiego:

	1
y=
	x

	2
y=
	x

y=4 x=4

	1
Domyślam się, że z góry będzie ograniczenie		, a z dołu?
	x

Jakub: Mam problem z calka ∫√2x−x² Przez co ją ruszyć ?

Mila: 2x−x²=−(x²−2x)=−{(x−1)²−1)=1−(x−1)² ∫√1−(x−1)²dx=... [x−1=t, dx=dt] ..=∫√1−t²dt Dalej poradzisz sobie?

Jakub: Mila I teraz rozbić to na 2 całki czy jak?

Mila: Możesz tak:

	1
∫√1−t2dt=∫U{1−t2}{√1−t2dt=∫		dt−∫U{t2}{√1−t2 dt=
	√1−t2

pierwsza z tablic, druga przez części albo II sposób t=sinu, dt=cosu du ∫√1−t²dt=∫√1−sin²u*cosu du=∫cos²u du

Jakub: Bo:

1−t2
	= √1−t2, tak?
√1−t2

Mila, a mogłabyś zobaczyć jak mam rozpisać 'ograniczenie'? Post z 17:19

Jakub:

	t2		1
∫		= | v = t2 u' =
	√1−t2		√1−t2

| v' = 2t u = arcsin t t² arcsint − ∫ 2t arcsin t dt I dalej mam tak robić? Czy odwrotnie wziąć przez części?

Jakub: Mógłby ktoś spojrzeć i doradzić co dalej?

Basia:

2
	= 4
x

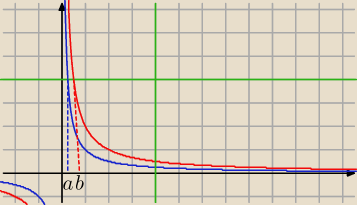
2 = 4x x = ¹₂ b = ¹₂

1
	= 4
x

1 = 4x x = ¹₄ a = ¹₄

	2		1
P = 4*12 + 1/2∫4		dx − [ 4*14 + 1/4∫4		dx ]
	x		x

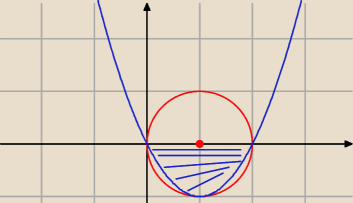
Basia: i po co Ty to tak skomplikowałeś ? P = pole półkola − pole niebieskiego =

π*12
	− [ −0∫2(x2−2x)dx ] =
2

π
	+ ∫2(x2−2x)dx
2

z tym sobie na pewno poradzisz

Mila: Miałam gości, ale widzę, że Basia wszystko wyjaśniła. Jakub całkę z 20:08 rozwiąż, przyda się.

Jakub: Mila A jak zapisać tego arcusa inaczej? Jako sin ⁻¹x i tak próbować?

maf: nie zapisywać inaczej tylko przez cześci

Basia: przez części wrócisz do całki początkowej; nic to nie da

	t2
∫		dt = t2 arcsint − ∫ 2t arcsin t dt
	√1−t2

jeżeli teraz zrobisz przez części to będzie

	1
u = arcsint u' =
	1−t2

v' = 2t v = t²

	t2
∫		dt = t2 arcsint − ∫ 2t arcsin t dt =
	√1−t2

	t2
∫U{t2}{√1−t2 dt = t2 arcsint − [ t2*arcsint − ∫		dt
	√1−t2

co daje

	t2		t2
∫		dt = ∫		dt
	√1−t2		√1−t2

co bez wątpienia jest prawdą, ale nic nie daje teraz nie mam już czasu, ale postaram się dzisiaj napisać jak to się liczy

Basia: całki:

	x2
J1 = ∫√a2−x2dx i J2 = ∫		dx
	√a2−x2

są całkami stowarzyszonymi i liczymy je razem Ty Jakubie podstawisz sobie potem a=1 i będziesz miał swoją całkę ∫√1−x²dx

	a2−x2
(1) J1 = ∫		dx =
	√a2−x2

	1		x2
a2∫		dx − ∫		dx =
	|a|√1 − (x/a)2		√a2−x2

	1
|a|*∫		dx − J2 = |a|*arcsinxa − J2
	√1−(x/a)2

(2) liczymy J₁ przez części

	1		x
u = √a2−x2 u' =		*(−2x) = −
	2√a2−x2		√a2−x2

v' = 1 v=x

	x2
J1 = x√a2−x2 + ∫		dx = x√a2−x2 + J2
	√a2−x2

mamy więc J₁ = |a|*arcsin^x_a − J₂ J₁ = x√a²−x² + J₂ −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− dodajemy stronami 2J₁ = |a|*arcsin^x_a + x*√a²−x² / :2

	|a|*arcsinxa + x*√a2−x2
J1 =		+ C
	2

czyli

	|a|*arcsinxa + x*√a2−x2
∫√a2−x2dx =		+ C
	2

J₁ = |a|*arcsin^x_a − J₂ J₁ = x√a²−x² + J₂ zatem x√a²−x² + J₂ = |a|*arcsin^x_a − J₂ 2J₂ = |a|*arcsin^x_a − x√a²−x² + C

	|a|*arcsinxa − x√a2−x2
J2 =		+ C
	2

czyli

	x2		|a|*arcsinxa − x√a2−x2
∫		dx =		+ C
	√a2−x2		2

Jakub: Basia − rozwiązanie które podałaś w poście o 22:32 jest o wiele prostsze i lepiej żebym tak tą całkę rozwiązał? Dziękuje bardzo za pomoc odnośnie tych całek stowarzyszonych!

	1
Odnośnie postu z 22:16, mógłbym poprosić o wytłumaczenie tego: "4 *		+" bo za bardzo
	2

tego nie rozumiem skąd się to wzięło

Basia: ad.1. jasne, że lepiej; przecież umiemy liczyć pole koła bez całki ad.2 tam można inaczej, ale wtedy więcej pisania między osiami a czerwoną linią mam prostokąt o wymiarach 4*b = 4*¹₂ + całka od tego potem odejmuję prostokąt o wymiarach 4*a = 4*¹₄ + całka pokażę Ci to na dwóch oddzielnych rysunkach można te prostokąty zignorować, ale wtedy będzie

	2		1
1/4∫1/24dx+1/2∫4		dx − 1/4∫4		dx
	x		x

Basia:

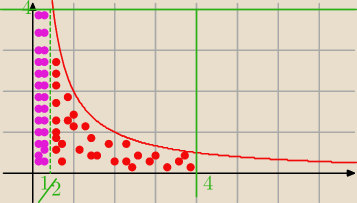
	2
P1 = pole prostokąta (fiolet) + obszar czerwony = 4*u{1}[2}+1/2∫4		dx
	x

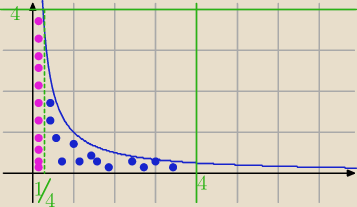
Basia: od P₁ muszą odjąć P₂ = prostokąt (filet) + obszar niebieski =

	1
4*14 + 1/4∫4		dx
	x

Jakub: Może głupio zabrzmi to pytanie, ale obszarem który mam policzyć jest obszar pomiędzy funkcją

	2		1
		a		ograniczony przez x=4 i y=4, tak?
	x		x

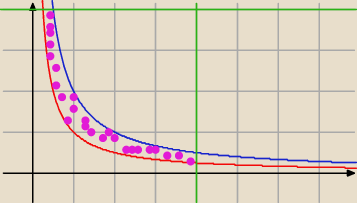
Basia: tak oczywiście; czyli to co na tym rysunku

Basia: kolory linii teraz zamieniłam

Jakub: Basia bardzo Ci dziękuje za pomoc i dokładne rozpisanie co z czego wynika!

Jakub: Mam jeszcze takie małe pytanie, bo chyba za bardzo nie widzę tych pól: Wpisałem sobie dla przykładu jakieś 3 funkcje do wolframu:

	1
x2 ,		x2 , 2x
	2

Wolfram pokazał wynik:

	x2		x2
0∫2		dx + 2∫4 (2x −		) dx
	2		2

i moje pytanie brzmi:

	x2
Dlaczego od 0 do 2 jest 0∫2		a nie 0∫2 2x − x2 dx ?
	2

asdf: daj link z wolframa

Jakub: http://www.wolframalpha.com/input/?i=area+between+x%5E2%2C+%281%2F2%29x%5E2%2C2x

Basia:

	x2
niebieskie y=
	2

czerwone y = x² zielone y= 2x Twój obszar to lila; składa się z dwóch częsci

	x2		x2
na lewo od czarnej kreski to 0∫2(x2−		) dx = 0∫2		dx
	2		2

	x2
na prawo od czarnej kreski to 2∫4(2x−		)dx
	2

Jakub: Kolejny raz dziękuję Basia!

Basia: Tam w tych stowarzyszonych jest błąd. W szóstej linijce ma być na końcu |a|*a*arcsin^x_a − J₂ no i dalej trzeba konsekwentnie poprawić

Mila: II sposób całka: ∫√1−x²dx ∫√1−x²dx=.. [x=sint, dx=cost dt, t=arcsin(x)]

	1
..=∫√1−sin2t*cos2t dt=∫cos2t=		∫(cos(2t)+1) dt=
	2

	1		1		1
=		*		sin(2t)+		t=
	2		2		2

	1		1
=		*2sint*cost+		arcsin(x)=
	4		2

	1		1
=		sin(arcsinx)*cos(arcsinx)+		arcsin(x)=
	2		2

	1		1
=		x*cos(arccos(√1−x2))+		arcsin(x)+C=
	2		2

	1		1
=		x√1−x2+		arcsin(x)+C
	2		2