Czy to jest dobrze? golo:

	lnx
Witam sprawdzam czy f jest rosnąca czy malejąca pochodnymi. No i pochodna z funkcji		w
	x

	(lnx)'*x − lnx*(x)'		1−lnx		1−x
odpowiedzi jest rozpisana tak:		=		=
	x2		x2		x2

	1−lnx		1−x
No i zastanawiam się z jakiej racji wychodzi		=
	x2		x2

	1−x
Dalej jest liczone		< 0 | * x2
	x2

1−x<0 x>1 i wychodzi ze dla x większych od jedynki zachodzi ta nierówność. Ale czy to jest dobrze jeśli juz wcześniej jest podejrzane? Wg mnie to błąd. Proszę o pomoc.

wredulus_pospolitus: oczywiście że błąd ... chyba że są jakieś 'ukryte' 'hinty' w treści zadania

golo:

	lnn
Zadanie ogólnie jest: rozstrzygnij czy szereg od 1 do ∞ ∑(−1)n		jest zbieżny
	n

bezwzględnie czy warunkowo. No i wychodzi, że bezwzględnie nie jest zbieżny. Zatem sprawdzamy

	lnn
z kryt. Liebnitza, czy jest warunkowo. No i 1 warunek, czyli czy lim		= 0 jest
	n

spelniony i teraz trzeba zobaczyć, czy warunek że ciąg ten jest malejący jest spełniony. Zatem

	lnn
liczymy pochodną z
	n

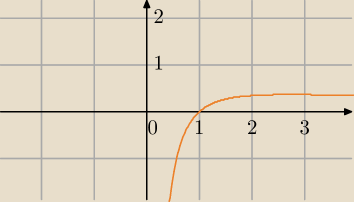
Mila: zał. x>0

	lnx		1   *x−(lnx)*1 x		1−lnx
(		)'=		=
	x		x2		x2

1−lnx
	>0⇔1−ln(x)>0⇔1>ln(x}
x2

ln(x)<1⇔ ln(x)<ln(e) i x>0⇔x>0 i x<e⇔ dla x∊(0,e) funkcja jest rosnąca dla x>e funkcja jest malejąca

	1
dla x=e funkcja ma maksimum ymax=
	e

golo: Dzięki wielkie, właśnie doszedłem do podobnych wniosków

Mila: Powodzenia.