Wyrażenia algebraiczne Kamix: Proszę o pomoc w rozwiązaniu podanej nierówności: 5x(x+3)(2−x)>0 Jest to nierówność 3 stopnia, co gorsza nie da się zastosować metody grupowania wyrazów... Jedyne co mi przychodzi do głowy to zastosowanie twierdzenia o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych, ale wydaje mi się, że istnieje dużo szybszy sposób poradzenia sobie z tą nierównością.... Stosując wspomniane twierdzenie zmarnowałbym naprawdę wiele czasu, gdyż po wymnożeniu dostaniemy liczbę 30, która ma sporo dzielników... Proszę o przejrzyste wytłumaczenie...

wredulus_pospolitus: ale co Ty chcesz grupować masz postać iloczynową czyli prawie koniec zadania pozostało jedynie: https://matematykaszkolna.pl/strona/142.html a najtrudniejszy (krok 1) masz już nawet za sobą

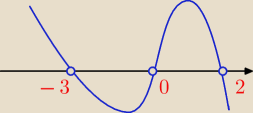
Kostek: −5x(x+3)(x−2)>0 x=0 lub x=−3 lub x=2 x∊(−∞,−3)∪(0,2)

Kamix: A no faktycznie, cóż mogę powiedzieć, zagapiłem się troszkę ; D Dziękuję ; P

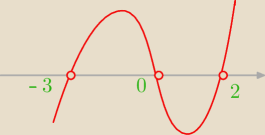
Kostek: chyba jednak coś źle zrobiłem 5x(x+3)(2−x)>0 −5x(x+3)(x−2)>0/ (−1) 5x(x+3)(x−2)<0 x=0 lub x=−3 lub x=2 x∊(−∞,−3)∪(0,2)

Boogeyman: 1 Wersja jest dobra, rysowanie wykresu zaczynamy z dołu bo współczynnik przy najwyższej potędze jest ujemny.

Boogeyman: W 2 wersji wyciągnąłeś minus przed nawias odpowiednio przemnożyłeś, odwróciłeś nierówność i też jest git