 1) 1+(y−1)3>0⇔
1+y3−3y2+3y−1>0⇔
y3−3y2+3y>0⇔
y*(y2−3y+3)>0⇔y>0 (wyrażenie y2−3y+3>0 dla y∊R)
Rozważymy dwa przypadki:
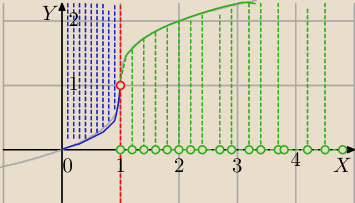
(1) x∊(0,1)
(2) x∊(1,∞)
ad(1)x∊(0,1)
logx(1+(y−1)3)≤logx(x)⇔
1+(y−1)3≥x
(y−1)3≥x−1
y−1≥3√x−1
y≥3√x−1+1 i y>0
ad(2) x∊(1,∞)
logx(1+(y−1)3)≤logx(x)⇔
1+(y−1)3≤x
(y−1)3≤x−1
y−1≤3√x−1
y≤3√x−1+1 i y>0
1) 1+(y−1)3>0⇔
1+y3−3y2+3y−1>0⇔
y3−3y2+3y>0⇔
y*(y2−3y+3)>0⇔y>0 (wyrażenie y2−3y+3>0 dla y∊R)
Rozważymy dwa przypadki:
(1) x∊(0,1)
(2) x∊(1,∞)
ad(1)x∊(0,1)
logx(1+(y−1)3)≤logx(x)⇔
1+(y−1)3≥x
(y−1)3≥x−1
y−1≥3√x−1
y≥3√x−1+1 i y>0
ad(2) x∊(1,∞)
logx(1+(y−1)3)≤logx(x)⇔
1+(y−1)3≤x
(y−1)3≤x−1
y−1≤3√x−1
y≤3√x−1+1 i y>0