funkcja kwadratowa i wzory Viete'a gamer: Znajdź wartości parametru k, dla których funkcja f(x) = x²+kx+9 ma dwa rozwiązania większe od 2 Chciałbym rozwiązać to zadanie wykorzystując wzory Viete'a. Więc daję warunki: Δ>0 ∧ x₁+x₂>4 ∧ x₁x₂>4 O ile ten warunek na sume jest OK, o tyle ten na iloczyn już nie działa. Gdzieś mam błąd w rozumowaniu i prosiłbym o wskazanie gdzie on jest

Aga1.: Funkcja kwadratowa ma 2 miejsca zerowe większe od 2 gdy Δ>0 i f(2)>0 i x_w>2

gamer: dzięki, ten sposób znam i rozumiem. Ale można też wykorzystać wzory Viete'a i to teraz chciałbym zrozumieć.

gamer: up

gamer: pomoże ktoś?

pigor: ... . Znajdź wartości parametru k, dla których funkcja f(x) = x²+kx+9 ma dwa rozwiązania większe od 2 . −−−−−−−−−−−−−−−−−−−−−−−−−−−−−− a więc Δ=k²−36 >0 i x₁ >2 i x₂ >2 ⇔ |k| >6 i x₁−2 >0 i x₂−2 >0 ⇔ ⇔ (*) (k<−6 lub k>6) i (x−1−2)(x₂−2)>0 i x₁−2+x₂−2>0 ⇒ ⇒ x₁x₂−2(x₁+x₂)+4 >0 i x₁+x₂>4, to stąd i wzorów Viete'a ⇔ ⇔ 9−2k+4 >0 i k >4 ⇔ 2k<13 i k>4 ⇔ 4< k< 6,5, więc stąd i z (*) ⇔ ⇔ 6 < k < 6,5, czyli k∊(6 ; 6.5) . ...

gamer: pigor, dziękuję za poświęcenie czasu, ale nie chodziło mi o rozwiązanie tego zadania, bo rozwiązań można kilka znaleźć w sieci wiem jak to wszystko rozpisać, ale nie rozumiem warunku z iloczynem. Ja to rozumiem w ten sposób: skoro dwa miejsca zerowe są większe od dwóch, to logiczne jest że ich suma jest większą od 4 ( i ten zapis jest prawidłowy ) oraz logiczne jest też dla mnie że ich iloczyn też będzie większy od 4 ( i to już nie jest dobre rozumowanie i właśnie nie wiem dlaczego )

delta: ... matko ducha ... pigor znów się uchlał −:(

5-latek: Skoro maja byc >2 to x₁>2 i x₂>2 to x₁−2>0 x₂−2>0 Teraz wyrazenia x₁−2 a takze x₂−2 beda dodatnie gdy 1. Suma tych wyrazen bedzie dodatnia czyli (x₁−2)+(x₂−2)>0 2. Iloczyn tych wyrazen bedzie dodatni czyli (x₁−2)(x₂−2)>0 3. Dodaj do tego 3 warunek delta >0 rozwiaz sobie to A teraz masz podany warunek w zadaniu ze dwa miejsca zerowe maja byc wieksze od 2 To wobec tego narysuj sobie ta parabole (ramiona w gore ) .Zaznacz na wykresie te miejsca zerowe >2 Zobaczysz wtedy ze wiercholek paraboli musi byc >2 . teraz sie zastanow jaki jest iloczyn dwoch miejc zerowych ( beda to miejsca zerowe dodatnie ) przy tak podanych warunkach zadania . Czy bedzie >4 ?

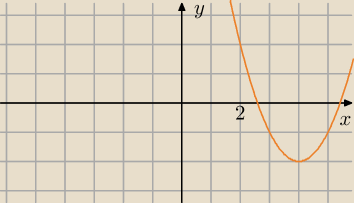
gamer: więc będzie to wyglądało mniej więcej tak. odpowiadając na pytanie czy będzie >4, nadal mi się wydaje, że tak będzie. Mógłbyś wyjaśnić dlaczego tak nie będzie?

5-latek: I dobrze CI sie wydaje ze bedzie Ja tylko zadalem CI pytanie . czy bedzie >4 ?. Juz z tego rysunku widac ze bedzie . Widzisz ze czasami pomaga w zrozumieniu prawidlowo wykonany rysunek. Czesc

gamer: iloczyn na pewno będzie większy od 4

	c
dlatego dałem warunek x1x2 > 4 ⇔		> 4
	a

ale z tego nie wychodzi poprawny przedział i wokół tego drążę ciągle ten temat.

pigor: ... uparłeś się jak osioł, i tracisz tylko czas, bo "twój" warunek x₁x₂=9>4 jest tu spełniony dla k∊R , jest jednak nie wystarczający, bo może być np. x₁=1,5 i x₂=3, a wtedy także iloczyn x₁x₂>4 i co , dlatego patrz na warunki Aga1 lub "uchlanego" pigora) tyle ....

5-latek. : To ze bedzie >4 to jest oczywiste . Prawidlowy przedzial to wyjdzie CI z tych 3 warunkow Ale tak samo iloczyn bedzie >4 gdy pierwiastki beda wieksze od3 Mozemy tylko stwierdzic ze iloczyn taki bedzie, jaki bedzie ten przedzial to trzeba policzyc warunek na iloczyn to nie jest x₁*x₂>4 tylko (x₁−2)(x₂−2)>0 i ztego warunku wyliczysz do jakiego przedzialu nalezy k . Ale to jest jeden z warunkow (x₁−2)(x₂−2)>0 ⇔x₁x₂=2x₁−2x₂+4>0⇔x₁x₂−2(x₁+x₂)+4>0

	c		−b
Teraz dopiero korzystasz ze wzoro viete a ze x1x2=		i x1+x2=
	a		a

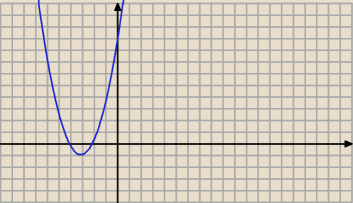
aniabb: wstawiłam k=6.3 i obrazek jakoś nie pasuje ;> chyba jednak te k ∊ (−6,5;−6)

gamer: dzięki chłopaki, ale dla mnie to i tak jest bez sensu. pigor, " x₁=1,5 i x₂=3, a wtedy także iloczyn x1x2>4 i co " wtedy także suma x₁+x₂ > 4 i co? i jednak można tak zapisać.

aniabb: u pigora zniknął minus x₁ + x₂ = −k

pigor: ..., a być może, że coś spieprzyłem pisząc on line i nie będą szukał co i jak , bo olewam już twój problem, a i tak na pewno nie zabrałbym się za niego wzorami Viete'a .

aniabb: reszta jest OK..tylko tego minusa zabrakło wtedy wychodzi k>−6.5 oraz k<−6 no i z delty k<−6 lub k>6

pigor: ... , dzięki ... aniabb .

aniabb: wtedy wychodzi k>−6.5 oraz k<−4 no i z delty k<−6 lub k>6

gamer: powiedzcie mi tylko dlaczego ten warunek na sume x₁+x₂ > 4 jest wystarczający, a ten na iloczyn już nie jest. przecież jak napisał pigor może być x₁=1,5 i x₂=3 i wtedy suma też jest większa niż 4 wiem że was trochę wymęczyłem, ale tak to jest jak czegoś się nie rozumie. dzięki wszystkim, szczególnie pigorowi, który już stracił cierpliwość

aniabb: oba są niewystarczające

pigor: ... a kto ci powiedział, że warunek na sumę jest wystarczający , na pewno nie ja , dlatego jak widzę szkoda mojego czasu tu i teraz, więc zmywam się już stąd ...

aniabb: pigor nie uzywał iloczynu x₁ • x₂ >4 tylko (x₁−2)(x₂−2)>0

gamer: x₁>2 ∧ x₂>0 ⇔ x₁−2>0 ⋀ x₂−2>0 x₁−2+x₂−2 > 0 ⇔ x₁+x₂ > 4

gamer: czyli suma jest większa od 4

aniabb: tak