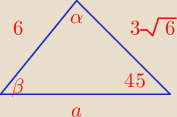
Planimetria bezendu: W trójkącie dwa boki mają długość 6cm i 3√6 cm Naprzeciw boku o długości 6 cm jest kąt o mierze 45⁰ Oblicz pozostałe katy

6		3√6
	=
sin450		sinβ

6		3√6
	=
√2   2		sinβ

6sinβ=3√3

	√3
sinβ=
	2

sinβ=60 α=180−60−45=75 W odpowiedziach jednak jeszcze jest podany drugi trójkąt o katach 120⁰ ,15⁰, 45⁰ z czego to wynika ?

Godzio:

	√3
Pewnie dlatego, że sinβ =		ma dwa rozwiązania, β = 60o lub β = 120o
	2

(sinβ = 60 jest złym zapisem, ale to chyba wiesz )

Aga1.:

	√3
sinβ=		⇒β=600 lub β=1800−600=1200
	2

bezendu: Godzio czyli w tego typu zadaniach trzeba korzystać ze wzorów redukcyjnych i mogą być dwa rozwiązania ?

bezendu: @Aga1 czemu liczysz 180⁰−60²=120⁰ przecież znamy jeszcze jeden kąt 45⁰ ?

Godzio:

	√3
Niekoniecznie wzory redukcyjne, po prostu trzeba wiedzieć, że sinα =		ma dwa
	2

rozwiązania w przedziale (0,π)

bezendu: Ok dzięki

Saizou : albo z wykresów

bezendu: Jeszcze jedno pytanie ?

	√3
czyli żeby to już poprawnie to należy rozwiązać równanie sinx=		w przedziale <0,2π>
	2

	√3
sinx=
	2

	π
sinx=
	3

	π		π		2
x=		lub π−		=		π
	3		3		3

czyli sin60⁰ lub sin120⁰ tak ?

Godzio: Jeżeli dalej mówimy o trójkącie to w przedziale (0,π) Reszta ok

bezendu: a no tak racja (0,π) bo trójkąt nie ma raczej 360^o