Geomteria
Piotrek:
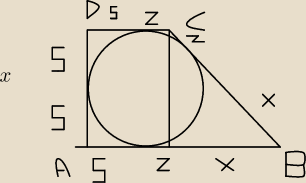
Na okręgu o promieniu długości 5 opisano trapez prostokątny, którego najkrótszy bok ma długość
7,5. Oblicz pole trapezu.
Mam nadzieję, że tu coś widać (z to jest odleglosc od punktu stycznosci do konca ramienia)
krótszy bok ma 7,5 więc z=2,5
x oznaczylem jako odleglosc od punktow stycznosci wiec
(x−z)
2+10
2=(x+z)
2
| | 25 | |
x2−5x+254+100=x2+5x+ |
| |
| | 4 | |
x=10
P=(5+x+z+5+z)*
102=125
czy to jest dobre rozwiązanie?
25 sie 16:13
Piotr 10: Wg mnie najkrótszy bok to będzie odcinek IDCI Dlaczego?
Na pewno IABI>IDCI.
IADI=10
a więc ICBI>10
i mi wyszło, że P=76,5[j2], ale pewny do tego to nie jestem
25 sie 17:45
ZK: | | 7,5+15 | |
Ptr= |
| *10 [j2] . Dlusza podstawa AB powinna CI wyjsc 15[j] |
| | 2 | |
25 sie 18:39
Piotrek: ZK dobrze ci wyszło, dlaczego dłuższa podstawa 15?
Piotr 10 według mojego rysunku najkrótszy bok to własnie DC, tak na intuicje ale dlaczego to
nie wiem
25 sie 19:59
Kostek:
@Pioterek a mógłbyś wstawić zdjęcie tego zadania bo z Twoich oznaczeń nic nie widać ?
25 sie 20:00
25 sie 20:05
Kostek: @Piotrek chodziło mi raczej o zdjęcie tego zadania z książki ?
25 sie 20:12
Piotr 10: Piotrek ja już nie myślę. Po prostu DC jest najkrótszym, bo mamy 4 boki w czworokącie.
Jeden bok to wysokość( ma on 10 cm, a więc jest dluzszy od 7,5 cm), teraz mamy AB podstawę ona
jest dluższa on podstawy DC. Bok CB jest dluzszy od 10 bo jak poprawdzisz prosta prostopadla z
wierzcholka C to stworzy się trojkat prostokatny, i tutaj powinienes zauwazyć ten Δ
prostokątny.
I wysuń odpowiednie wnioski
25 sie 20:23
25 sie 20:29
Piotr 10: Piotrek rozumiesz dlaczego krótsza podstawa równa się 7,5 ?
25 sie 20:31
25 sie 20:31
Piotrek: to już rozumiem natomiast nie wiem dlaczego dłuższa ma długość 15
25 sie 20:31
Piotr 10: Zbiór Pazdro

. Też go przerabiałem

25 sie 20:32
Piotr 10: Ok to ja spróbuję to zrobić jeszcze raz, wcześniej błąd jakiś mi się wkradł
25 sie 20:32
Piotr 10: a+b=c+d
a−krótsza podstawa
b−dłuższa podstawa
c−wysokość
d−czwarty bok
c=10 a=7,5
7,5+b=10+d
d=b−2,5
Teraz tworzę trójkąt prostokątny. Prowadzę z wierzchołka C prosta prostopadła do prostej AB.
d
2=10
2+(b−7,5)
2
(b−2,5)
2=100+b
2−15b+56,25
b
2−5b+6.25=100+b
2−15b+56,25
10b=150
b=15

25 sie 20:39
Mila:
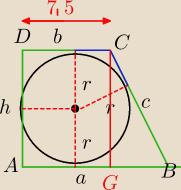
r=5
h=2r=10
DC=b=7,5
BC=c,
a+b=c+h sumy boków przeciwległych są równe.
a+7,5=c+10⇔c=a−2,5
w ΔCGB: c=a−2,5; |GB|=a−7,5
c
2=GB
2+h
2
(a−2,5)
2=(a−7,5)
2+10
2
a
2−5a+6,25=a
2−15a+56,25+100⇔
10a=150
a=15
| | 15+7,5 | |
P= |
| *10=22,5*5=112,5 |
| | 2 | |
P=112,5j
2
25 sie 20:48
Piotrek: mila jak robic takie fajne rysunki
25 sie 20:51
ZK: 1. Narysuj prosta prostopadla przechodzaca przez srodek okregu wpisanego w ten trapez i dwie
podstawy i napisz oznaczenia Np. punkt przeciecia z bokiem DC np przez E a punktk przeciecia z
bokiem AB przez F . Srodek okregu standart przezO
2. Narysuj proste OC i OB .Zauwaz ze prosta OC jest dwusieczna kata ECB a prosta BO jest
dwusieczna kata FBC
3> wykaz ze trojkaty OEC i OFB sa podobne
4. jesli juz to dowiedziesz to zauwazysz ze mozna ulozyc taka proporcje
FB

F=OE:EC zdanych zadania EC=2,5 ztego wylicz FB . Masz juz wszystkie dane do policzenia
.
5. Wiec dlugosc boku AB=AF+FB=5+wyliczone FB =15
6. policz pole
25 sie 21:04
ZK: | | FB | | OE | |
Nie wiem czemu takie duze oczy wyszly ale tam ma byczapisze to inaczej |
| = |
| |
| | OF | | EC | |
25 sie 21:08
Mila:
Rysunki − korzystaj z opcji "rysuj", zaczynasz od okręgu.
25 sie 21:09
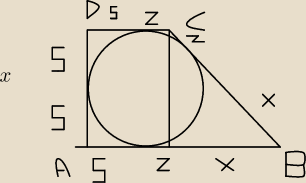 Na okręgu o promieniu długości 5 opisano trapez prostokątny, którego najkrótszy bok ma długość
7,5. Oblicz pole trapezu.
Mam nadzieję, że tu coś widać (z to jest odleglosc od punktu stycznosci do konca ramienia)
krótszy bok ma 7,5 więc z=2,5
x oznaczylem jako odleglosc od punktow stycznosci wiec
(x−z)2+102=(x+z)2
Na okręgu o promieniu długości 5 opisano trapez prostokątny, którego najkrótszy bok ma długość
7,5. Oblicz pole trapezu.
Mam nadzieję, że tu coś widać (z to jest odleglosc od punktu stycznosci do konca ramienia)
krótszy bok ma 7,5 więc z=2,5
x oznaczylem jako odleglosc od punktow stycznosci wiec
(x−z)2+102=(x+z)2
 . Też go przerabiałem
. Też go przerabiałem 

 r=5
h=2r=10
DC=b=7,5
BC=c,
a+b=c+h sumy boków przeciwległych są równe.
a+7,5=c+10⇔c=a−2,5
w ΔCGB: c=a−2,5; |GB|=a−7,5
c2=GB2+h2
(a−2,5)2=(a−7,5)2+102
a2−5a+6,25=a2−15a+56,25+100⇔
10a=150
a=15
r=5
h=2r=10
DC=b=7,5
BC=c,
a+b=c+h sumy boków przeciwległych są równe.
a+7,5=c+10⇔c=a−2,5
w ΔCGB: c=a−2,5; |GB|=a−7,5
c2=GB2+h2
(a−2,5)2=(a−7,5)2+102
a2−5a+6,25=a2−15a+56,25+100⇔
10a=150
a=15
 F=OE:EC zdanych zadania EC=2,5 ztego wylicz FB . Masz juz wszystkie dane do policzenia
.
5. Wiec dlugosc boku AB=AF+FB=5+wyliczone FB =15
6. policz pole
F=OE:EC zdanych zadania EC=2,5 ztego wylicz FB . Masz juz wszystkie dane do policzenia
.
5. Wiec dlugosc boku AB=AF+FB=5+wyliczone FB =15
6. policz pole