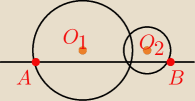
koła ?: Przez punkt wspólny dwóch przecinających się okręgów o środkach O1 i O2 poprowadzono sieczną równoległą do prostej O1O2. Przecięła ona jeden okrąg w punkcie A, natomiast drugi− w punkcie B. Wykaż, że: a) |O1O2|= \frac{1}{2}|AB| b) odcinek AB jest dłuższy od wszystkich innych odcinków siecznych przechodzących przez punkt C.

?: podpunkt a) mam z błędem, chodzi o: a) |O₁O₂|= 1/2|AB|

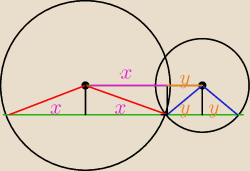
Aga1.: IABI=2x+2y IO₁O₂I=x+y

?: a podpunkt b) ?

ZK: W ktorym miejscu jest punkt C

?: w którymś z okręgów?

?: ...

?: może ktoś się jeszcze skusi..