geometria zadanie: W wierzchołkach kwadratu o boku 1 km znajduja sie 4 domy. Czy mozna zbudowac siec dróg o łacznej długosci mniejszej od 2√2 km, umozliwiajaca dojscie z kazdego domu do kazdego innego? Odpowiedz: Tak. Mozna zbudowac siec dróg o łacznej długosci równej 1+√3 km. W tym celu zamiast narzucajacego sie połaczenia domów ze srodkiem kwadratu, nalezy utworzyc dwa rozwidlenia. Z kazdego z nich powinny wychodzic 3 drogi tworzace katy 120^o. Dwie z tych dróg powinny prowadzic do dwóch sasiednich wierzchołków kwadratu, a trzecia do drugiego rozwidlenia. nie wiem jak do tego dojsc nawet nie umiem narysowac dobrze rysunku.

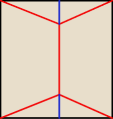
Janek191: Długość niebieskiego odcinka

x
	= tg 30o
12

	1		√3		√3
x =		*		=
	2		3		6

Długość czerwonego pionowego odcinka

	√3
1 − 2x = 1 −
	3

Długość czerwonego skośnego odcinka

	√3		1		3		1		12
y2 = (		)2 + (		)2 =		+		=		= 13
	6		2		36		4		36

więc

	√3
y = √13 =
	3

Długość wszystkich czerwonych odcinków

	√3		√3
4*y + 1 − 2x = 4*		+ 1 −		= √3 + 1
	3		3

zadanie: dziekuje ale skad mam wiedziec, ze w tym trojkacie bedzie 30^o?

zadanie: juz wiem bo te drogi tworza kat o mierze 120^o.

Basia: niezupełnie; to już jest odpowiedź trzeba dojść do tego, że to będzie właśnie 120^o

zadanie: a jak do tego dojsc?