Nierówność problem...
Mateusz:
Witam posiadam jedno pytanie.
Mam taką oto nierówność :
ustalam dziedzinę :
3x+5=0
3x=−5 /:3
x=−
53
D=R\−
53
teraz mnożę nierówność na krzyż i wychodzi :
3x−2<0
3x<2 /:3
x<
23
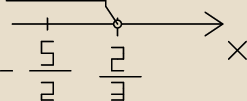
zaznaczam na osi x i wychodzi mi że wykluczenie dziedziny jest <0 jak poprawic wykres tak aby
wyszedł dobrze.
Saizou :
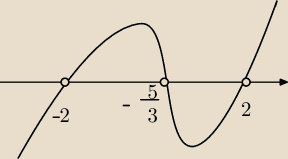
jaki krzyż


jest to nierówność wymierna zatem nie wiesz czy mnożysz przez dodatni mianownik, lepije
skorzystać z twierdzenia o zamianie ilorazu na iloczyn (czy jakoś tak)
| x2−4 | |
| <0 /(3x+5)2 zawsze dodatnie |
| 3x+5 | |
(x
2−4)(3x+5)<0
(x−2)(x+2)(3x+5)<0
PW: @Mateusz: Coś z tym "mnożeniem na krzyż" zmąciłeś. Nijak nie wiadomo, skąd pojawiło się
3x−2<0.
Tutaj nie ma co mnożyć na krzyż, skoro po prawej stronie nierówności było zero.
Mamy ułamek
który ma być ujemny. Ponieważ iloraz i iloczyn mają taki sam znak (oba są ujemne albo oba
dodatnie, albo oba są zerem dla tych x, dla których ułamek ma sens), możemy napisać tak:
| | x2−4 | |
|
| <0 ⇔ (x2−4)(3x+5)<0 ⇔(x−2)(x+2)(3x+5)<0. |
| | 3x+5 | |
Saizou w końcu zrobił to "modniejszym ostatnio" sposobem pomnożenia obu stron nierówności
przez kwadrat mianownika, który na pewno jest dodatni i doszedł do tej samej nierówności.
Masz więc dwa sposoby (dwie różne argumentacje) prowadzące do tego samego wyniku.
| | 5 | |
Dziedzina ustalona na początku jest poprawna: x≠− |
| , i tego już nie ruszamy, nic nie jest |
| | 3 | |
| | 5 | |
w stanie zmienić dziedziny. A rozwiązanie oczywiście nie może zawierać liczby − |
| . |
| | 3 | |
Odczytujemy je z wykresu zrobionego przez Saizou.
 Witam posiadam jedno pytanie.
Mam taką oto nierówność :
Witam posiadam jedno pytanie.
Mam taką oto nierówność :
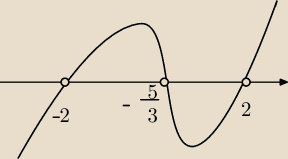 jaki krzyż
jaki krzyż
 jest to nierówność wymierna zatem nie wiesz czy mnożysz przez dodatni mianownik, lepije
skorzystać z twierdzenia o zamianie ilorazu na iloczyn (czy jakoś tak)
jest to nierówność wymierna zatem nie wiesz czy mnożysz przez dodatni mianownik, lepije
skorzystać z twierdzenia o zamianie ilorazu na iloczyn (czy jakoś tak)