wielokaty foremne zadanie: Dziewieciokat A₁A₂A₃...A₉ jest foremny. Wyznaczyc miary katow trojkata a) A₁A₃A₇ jak to zrobic?

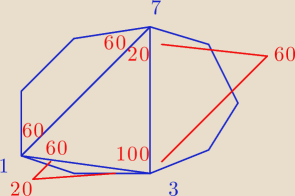
Godzio: S_k = 180 * (n − 2) = 180 * 7 = ... (wzór na sumę kątów w wielokącie)

Sk
	= miara jednego kąta
9

Jak coś nie jasnego to pytaj póki jeszcze jestem

zadanie: odpowiedz jest taka katy przy wierzchołkach A₁, A₃, A₇ maja miary odpowiednio 80^o, 60^o, 40^o

zadanie: S_k=1260^o

1260o
	=140o czyli miara jednego kata wynosi 140o to rozumiem a jak pozniej wyznaczyc
9

tamte katy ?

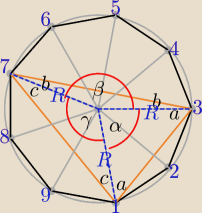
Bogdan: R − promień okręgu opisanego na 9−kącie 360^o : 9 = 40^o, α = 2*40^o = 80^o, β = ..., γ = ... Szukane miary kątów: a+b, b+c, a+c

zadanie: β=160^o; γ=120^o a+c=80^o a+b=60^o b+c=40^o

zadanie: dziekuje

zadanie: dla ktorych liczb naturalnych n istnieje n kat wypukly ktorego kazdy kat wewnetrzny ma miare 60^o lub 160^o? ja robie tak: (n−2)*180^o=60^on (n−2)*3=n 3n−6=n 2n=6 n=3 czyli trojkat oraz (n−2)*180^o=160^on 9n−18=8n n=18 czyli osiemnastokat wypukly a w odp. jest dla n=3, 8, 13 i 18. co robie zle?

zadanie: moge prosic o wytlumaczenie?

Godzio: No, pomyliłem się, po lewej stronie powinny być kąty 40^o, a nie 60^o

	180o * 6
W tym drugim zadaniu jest oczywiście błąd, bo dla n = 8 mamy miarę		= 135o
	8

A dla n = 13 coś koło 152^o

zadanie: dziekuje

zadanie: Dany jest dwunastokat foremny A1_A2A3 ...A12. Dla podanych dwóch przekatnych wskazac trzecia przekatna przechodzaca przez ich punkt przeciecia. a) A₁A₇, A₃A₉ po narysowaniu nie ma problemu ale czy mozna to jakos obliczyc o jakie przekatne chodzi?

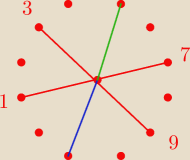
Godzio: Mam taką propozycję: Teraz prowadzisz dwa odcinki od punktu przecięcia do podejrzanych wierzchołków, i udowadniasz, że między tymi odcinkami jest kąt 180^o

Mila: Zadanie z godziny 12:45 Suma kątów : (n−2)*180^o Pewna liczba kątów wewnętrznych ma miarę 60^o a pewna ma miarę 160^o. k*60^o+(n−k)*160^o=(n−2)*180^o zał. k∊N, k≤n 60k+160n−160k=180n−360 −100k−20n=−360 100k+20n=360 20n=360−100k n=18−5k zał. n∊N₊ i n≥3 ⇔3≤18−5k⇔5k≤15⇔k≤3 i k∊N k=0 n=18 k=1 n=18−5=13 k=2 n=18−2*5=8 k=3 n=18−5*3=3 Odp. n∊{3,8,13,18}

zadanie: ok dziekuje Pewna liczba kątów wewnętrznych ma miarę 60^o a pewna ma miarę 160^o ale jednoczesnie w jednym n−kacie lub w kazdym osobno i ja to wlasnie wczesniej obliczylem bo ja myslalem, ze to w jednym ma byc 60⁰ a w drugim 160⁰.

Mila: Tam było słowo "lub".