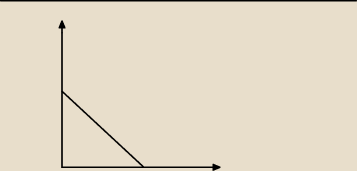
Równanie różniczkowe Kubek: Proszę o rozwiązanie ∫∫(x+y−2)dxdy na obszarze trójkąta x=2 i y=2

AS: Równanie różniczkowe?

ejendi: pole trójkąta ah/2=2*2/2=2 całka pojedyńcza y=−x+2 0<x<2 ∫(−x+2)dx=−x²/2+2x=−4/2+4=2 całka podwójna się zeruje, nie wiem dlaczego ∬(x+y−2)dxdy 0<x<2 i 0<y<2 ∬(x+y−2)dxdy=∫(∫(x+y−2)dy)dx=∫(xy+y²/2−2y)|dx =∫(2x−2)dx=2∫(x−1)dx=2(x²/2−x)=2(2−2)=0