z parametrem Jaruś: Dla jakich wartości parametru m równanie sin²x + sinx + m = 0 ma rozwiązanie?

use: policz delte ( musisz jednak uwzglednic fakt że sinx∊<−1;1>)

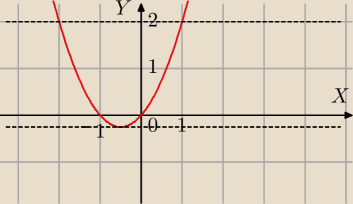
Mila: sin²x + sinx + m = 0 sin²x + sinx =− m sinx=t i t∊<−1,1> f(t)=t²+t parabola skierowana ramionami do góry

	−b		−1		−1
tw=		=		∊<−1,1> zatem najmniejsza wartość f(t) ma w tym przedziale dla t=
	2a		2		2

	−1		−1		−1
yw=(		)2+(		)=		najmniejsza wartość f(t) w przedziale <−1,1>
	2		2		4

Największa dla t=1 f(1)=2

−1
	≤−m≤2
4

1
	≥m≥−2
4

	1
m∊<−2,		>
	4

ZKS: Można też tak f(x) = sin²(x) + sin(x) + m sin(x) = t ∊ [−1 ; 1] f(t) = t² + t + m Aby ta funkcja miała rozwiązanie to [f(−1) ≥ 0 ∨ f(1) ≥ 0] ∧ Δ ≥ 0 f(−1) = m ⇒ m ≥ 0 ∨ f(1) = 2 + m ⇒ m ≥ −2 ⇒ m ∊ [−2 ; ∞)

	1
Δ = 1 − 4m ⇒ 1 − 4m ≥ 0 ⇒ m ≤
	4

	1		1
m ∊ [−2 ; ∞) ∧ m (−∞ ;		] ⇒ m ∊ [−2 ;		].
	4		4