Ciąg liczbowy calineczka: a) znajdź wyraz a₂6 ciągu arytmetycznego, w którym a₂ = 7 i a₃ = 5. b) znajdź a₁ oraz różnicę ciągu arytmetycznego, w którym a₁0 = −12 i a₅ = 3.

wredulus_pospolitus: a₃ − a₂ = r a₁ = a₂ − r a₂₆ = a₁ + 25*r

wredulus_pospolitus: a₁₀ = a₁ + 9r a₅ = a₁ + 4r a₁₀ − a₅ = ... czemu się równa dokończ

bezendu: a) a₁+r=7 /(−1) a₁+2r=5 −a₁−r=−7 a₁+2r=5 r=−2 a₁−2=7 a₁=9 a₂₆=9+(26−1)*(−2) a₂₆=9+25(−2) a₂₆=−41 b) a₁+9r=−12 / (−1) a₁+4r=3 −a₁−9r=12 a₁+4r=3 −5r=15 5r=−15 r=−3 a₁−27=−12 a₁=15

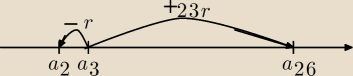
Gustlik: Można prościej − bez zbędnych układów równań, na JEDNEJ niewiadomej. a) znajdź wyraz a26 ciągu arytmetycznego, w którym a2 = 7 i a3 = 5. b) znajdź a1 oraz różnicę ciągu arytmetycznego, w którym a10 = −12 i a5 = 3. ad a) a₃−a₂=r 5−7=r r=−2 a₂₆=a₃+23r=5+23*(−2)=5−46=−41 Trochę przypomina to jazdę pociągiem. Można sobie wyobrazić ciąg jako linię kolejową, a kolejne wyrazy to jak kolejne stacje na tej linii, np. a₁ − stacja nr 1, a₂ − stacja nr 2 itd. Najpierw wsiadamy na stacji 3 (wyraz a₃) i jedziemy na stację 2 (wyraz a₂) − cofamy się o jeden przystanek czyli o jedną różnicę (1r) czyli a₃−a₂=r, tak wyznaczamy róznicę. Potem wsiadamy na stacji 3 (a₃) i jedziemy na stację 26 (a₂₆) − trzeba podjechać o 23 przystanki do przodu, czyli dodać 23r, stąd a₂₆=a₃+23r, mając dwa wyrazy do wyboru wybieramy ten leżący bliżej szukanego, czyli a₃. Nie ma sensu liczyć a₁, po co cofać się do stacji początkowej, skoro stacja 3 leży bliżej stacji 26, czy w życiu też tak robimy korzystając z usług PKP? Ta "kolejowa" metoda bardzo ułatwia życie. Skojarzyć hasło "ciągi−pociagi" i po kłopocie.

Gustlik: ad b) znajdź a1 oraz różnicę ciągu arytmetycznego, w którym a10 = −12 i a5 = 3. Też metodą "kolejową": a₁0−a₅=5r jedziemy ze stacji 10 na stację 5 − odległość to 5 "przystanków", czyli 5r −12−3=5r −15=5r /:5 r=−3 Teraz a₁ − wsiadamy na stacji 5, bo leży bliżej stacji 1 i cofamy się o 4 "przystanki", czyli odejmujemy 4r: czyli a₁=a₅−4r a₁=3−4*(−3) a₁=3+12 a₁=15 Mamy a₁=15, r=−3