trojkaty Pat: Oblicz pole trojkata o bokach: 6cm, 10cm, 12cm.

aba: https://matematykaszkolna.pl/strona/503.html wzór Herona

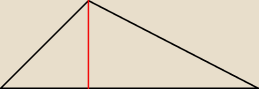
Janek191: Inny sposób: h − wysokość Δ x + (12 − x) = 12 Mamy x² + h² = 6² = 36 (12 − x)² + h² = 10² = 100 ; odejmujemy stronami (12 − x)² − x² = 64 144 − 24x + x² − x² = 64 24x = 80

	10
x =
	3

więc

	100		324 − 100		224
h2 = 36 − x2 = 36 −		=		=
	9		9		9

	4√14
h =
	3

	4√14
P = 0,5a*h = 0,5*12*		= 8√14
	3

====================================

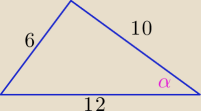aba: Jeszcze inny sposób

	102+122−662		13
z tw. kosinusów cosα=		= ....=
	2*10*12		15

	√56		2√14
sinα= √1−cos2α = √1−169225=		=
	15		17

	1		2√14
P=		*10*12*sinα= 60*		=8√14 [j2]
	2		15

aba:

	102+122−62		13
oczywiście ma być : cosα=		= ...=
	2*10*12		15

Gustlik: Oblicz pole trojkata o bokach: 6cm, 10cm, 12cm. Najprościej Heronem: Liczymy obwód Obw=6+10+12=28 cm

	1
p=		Obw=14 cm
	2

Pole P=√p(p−a)(p−b)(p−c)=√14(14−6)(14−10)(14−12)= =√14*8*4*2=√896=2*2*2*√14=8√14 Rozkładam 896 na czynniki w celu wyłączenia czynnika przez pierwiastek: 896 | 2 448 | 2 ⇒ 2 224 | 2 112 | 2 ⇒ 2 56 | 2 28 | 2 ⇒ 2 14 | 2 7 | 7 ⇒ √14