Wartość bezwzględna - sprawdzanie różniczkowalności Sever: f(x)=x|x−1| czy funkcja jest różniczkowalna w punkcie x0=1 Wiem jak liczyć normalną różniczkowalność, albo zwykłą pochodną z wartości bezwzględnej, ale nie mam pojęcia jak zabrać się za takiego typu zadanie z wartością bezwzględną.

pigor: ... policz sobie 2 granice jednostronne w definicji pochodnej x → ±1, to powinieneś wykazać, że nie są one równe, a to oznacza, że w x=1 dana funkcja f nie ma granicy, czyli nie jest ona w tym punkcie różniczkowalna . ...

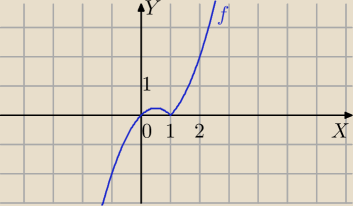
Mila: f(x)=x²−x dla x≥1

	(1+h)2−(1+h)−(12−1)
limx→1+		=1
	h

f(x)=−x²+x dla x<1

	−(1+h)2+(1+h)−(−12+1)		−1−2h−h2+1+h
limx→1−		=limx→1−		=−1
	h		h