nierownosci funkcji wymiernej. uki: Nierownosci funkcji wymiernej

1
	> 4x
x

	1
mnożymy przez mianownik i jest chyba 1 >4x2 dziele przez 4 i jest		> x2
	4

	1		1		1
czyli		> x u −		<x daje nam to X∊(−∞ ; −		) u ( 12 ; +∞) a w odp pisze w
	2		2		2

	1
ostatnim przedziale (0;		) Dlaczego? :<
	2

Aga1.: Mnożymy przez mianownik do kwadratu.

5-latek: Najpierw dziedzina Nie mozesz pomnozyc przez mianownik bo nie wiesz jakie jest x Co bedzie gdy x=0 lub gdy x bedzie ujemne ?

bezendu: x=0 Heteryk a x<0 zmieniasz znak

uki: czyli jak to bedzie wygladalo krok po kroku :C

ICSP: Schemat : 1. Ustalasz dziedzinę 2. Wszystko na lewą stronę 3. Sprowadzasz do wspólnego mianownika 4. Zamieniasz na iloczyn 5. Rozwiązujesz nierówność wielomianową 6. Podajesz odp 7. Sprawdzasz z dziedziną Przykład :

1
	> 4x , przy x ≠ 0
x

1
	− 4x > 0
x

1 − 4x2
	> 0
x

x(1 − 4x²) > 0 (2x−1)(2x+1)x < 0

	1		1
x ∊ (−∞ ; −		) ∪ (0 ;		)
	2		2

Janek191:

1
	> 4x ; x ≠ 0
x

1
	− 4x > 0
x

1		4x2
	−		> 0
x		x

1 − 4x2
	> 0
x

( 1 − 4x²)*x > 0 ( 1 − 2x)*(1 + 2x)*x > 0 x ∊ ( − ∞ ; −¹₂ ) ∪ ( 0; ¹₂) =============================

uki: mistrzeee o to mi wlasnie chodzilo dziekowac serdecznie

uki: Mam teraz takie cos :

3x−2
	> 0
x−3

Df − R= {3}

W(x)
	>0 ⇔W(x)*P(x) >0 (z tego co pamietam iz tylko posiadam zbiorek.)
P(x)

	3
wiec wychodzi ze x>		lub x>3
	2

	3
czyli powinno byc chyba (		; 3) u (3 ; +∞)
	2

	3
w odpowiedzi jest ze pierwszy nawias od ujemnej nieskonczonosci do		nie czaje dlaczego ?
	2

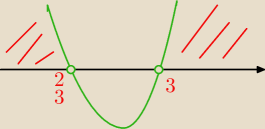
bezendu: (3x−2)(x−3)>0

	2		3
x=		a nie
	3		2

interesuję Cie to co jest nad osią (czerwone kreski)

	2
x∊(−∞,		)∪(3,∞)
	3

uki: Do tej pory wszystko przecwiczone dzieki

	1		1		x−3
Teraz nie wiem jak ruszyc		<		D x≠0 i to		> 1
	x		3		2x−1

ad.1 wiadome dac wszystko na lewo tylko nie wiem jak to dac we wspolnym l.m.

uki: nie pykne tego sam jednak ;c

bezendu: w czym masz znowu problem ? pokazywałem Ci dziś jak to rozwiązywać ?

x−3
	>1
2x−1

	1
D=R\{		}
	2

x−3
	−1>0
2x−1

x−3−(2x−1)
	>0
2x−1

dokończ

5-latek:

	1
Przeciez jak przeniesiesz		na lewa strone to nie bedzie tak jak zapisales/as tylko tak
	3

	1		1		3		x		3−x
		−		<0 −−−−−wspolny mianownik to 3x		−		<0 to		<0
	x		3		3x		3x		3x

Teraz moge skorzystac z tego ze znak ilorazu jest tali sam jak iloczynu (nie zmieni sie zwrot nierownosci) to (3−x)*3x<0 to 9x−9x²<0 Dostalismy nierownosc kwadratowa niepelna wiec nie liczymy delty tylko 9x(1−x)<0 Miejsca zerowe 9x=0 to x=0 i 1−x=0 to −x=−1 to x=1 Wspolczynnik przy x²=−9<0 to nierownosc ta jest <0 w przedziale (−nieskonczonosc ,−1)U(0,+nieskonczonosc ) Teraz widze ze 0 nie nalezy do dziedziny ani tez do rozwiazania tej nierownosci wiec jest OK Odpowiedz sobie na pytanie ?Jakie by bylo rozwiazanie tej

	1		1
nierownosci gdyby to byla nierownosc slaba czyli		{≤
	x		3

5-latek: Teraz widze ze TY tego nie zapisales tylko ta druga nierownosc to jest inny przyklad

uki: tam przy (3−x)*3x <0 ppowinno byc chyba 9x−3x² <0 ? pokazywales ale tamto sie lekko różnił;c.