funkcji o homograficznej o wzorze adrianooo :

	2x−3
Wykres funkcji o homograficznej o wzorze f(x)=		otrzymamy w wyniku przesuniecia
	x+2

	a
rownoleglego wykresu proporcjonalnosci odwroptnej y=		o pewnien wektor.
	x

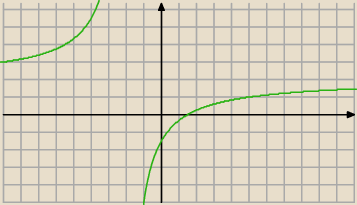
a)Wyznacz wzor proporcjonalnosci dwrotnej oraz wspołrzedne wektora przesuniecia b)Oblicz miejsce zerowe funkcji oraz wspolrzedne punktu przeciecia osi OY c)narysuj wykres funkcji d)podaj przedzialy monotonicznosci

bezendu:

	2x−3
f(x)=
	x+2

	2(x+2)−7		−7
f(x)=		=		+2
	x+2		x+2

b) 2x−3=0 2x=3

	3
x=
	2

2*0−3		−3
	=
0+2		2

	3
więc punkt przecięcia z osią OY =(0,−
	2

d) przedziały monotoniczności odczytasz z wykresu

Mila: a) wzór proporcjonalności

	−7
y=		, a=−7
	x

u^→=[−2,2] wektor przesunięcia Szkoda, że brak asymptot na rysunku (przerywana linią).

ICSP: i dziedziny brakuje

Mila: Adrian dopisze.

bezendu: D=R\{−2}

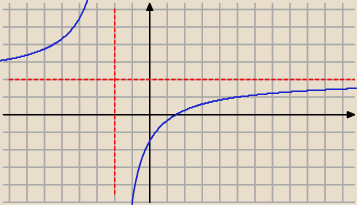
bezendu: a więc są i asymptoty x=−2 i y=2

Mila: Szkoda,że Adrian tego nie czyta.