okrag zadanie: punkt O jest srodkiem okregu wpisanego w trojkat ABC. wiadomo, ze kat AOB=katowi ACB +60^o.wyznaczyc miare kata ACB. odp. 60^o. rozwiazanie jest takie: punkt O laczymy z wierzcholkami ABC, oraz prosty rachunek na katach prowadzi do zaleznosci

	kat ACB
kat AOB=		+90o.
	2

	kat ACB
nie rozumiem skad to sie wzielo, ze kat AOB=		+90o ? moge prosic o wytlumaczenie?
	2

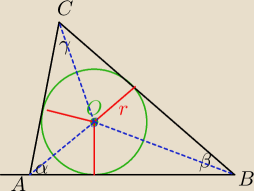
Mila: Środek okręgu wpisanego w trójkąt leży na przecięciu dwusiecznych kątów wewnętrznych trójkąta W ΔAOB:

1		1
	α+		β+∡AOB=180
2		2

α+β+γ=180 α+β=180−γ

1
	(α+β)+∡AOB=180
2

1
	(180−γ)+∡AOB=180
2

	1
90−		γ+∡AOB=180
	2

	1
−		γ+∡AOB=90
	2

	1		∡ACB
∡AOB=90+		γ⇔∡AOB=90+
	2		2

zadanie: dziekuje

Mila: Wyszło?

zadanie: tak juz rozumiem

zadanie: ale mam podobne i w polowie mam je dobrze bo nie rozumiem drugiej czesci rozwiazania zaraz je napisze

zadanie: tresc dotyczy tego samego zadania ale gdy O jest srodkiem okregu opisanego na trojkacie ABC. kat AOB=α; kat ACB=β korzystajac z twierdzenia o kacie srodkowym i wpisanym mam: α=2β oraz α=β+60^o stad β=60^o i to jest pierwsza czesc rozwiazania ktora rozumiem druga czesc mowi, ze β=100^o taki jest komentarz: Co prawda kat srodkowy ma miare dwa razy wieksza od kata wpisanego w okrag opartego na tym samym łuku, jednak w przypadku, gdy kat srodkowy jest wklesły (tzn. ma miare wieksza od 180^o) zapis kat AOB oznacza kat wypukły. W tym wypadku zaleznosc miedzy katem wpisanym i srodkowym przyjmuje postac kat AOB =360^o−2*(kat ACB) i tego nie rozumiem ostatecznie sa 2 mozliwosci β=60^o lub β=100^o.

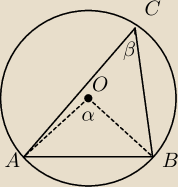
Mila: α=2β oraz α=β+60^o 2β=β+60 β=60 To jest jasne. Będzie drugi wpis.

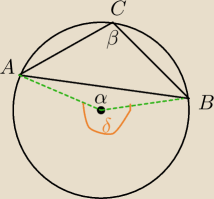
Mila: Rozważamy trójkąt o kącie β>90 β odpowiada kątowi środkowemu δ δ=2β α=360−2β i α=β+60 360−2β =β+60 300=3β β=100^o

zadanie: dziekuje

zadanie: dla ktorych liczb naturalnych n≥3 ponizsze danie jest prawdziwe a) dowolny n kat wpisany w okrag i majacy wszystkie boki rownej dlugosci jest foremny. dla n≥3 b) dowolny n kat wpisany w okrag i majacy wszystkie katy rownej miary jest foremny. tez chyba n≥3?tutaj nie jestem pewien da sie to jakos sprawdzic?

zadanie: ?

Mila: Środek okręgu opisanego na wielokącie leży na przecięciu symetralnych boków. b) n=3, tak, Δrównoboczny n=4 nie , bo prostokąt można wpisac w okrąg , a nie jest to wielokąt foremny. n=5 badaj , dalej.

zadanie: dla n=5 tak bo wydaje mi sie, ze kazdy pieciokat wpisany w okrag i majacy katy rownej miary jest foremny podobnie dla n=6 bi nie umiem znalezc przykladu, ze taknie jest

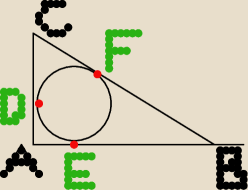
zadanie: wyznaczyc polozenie punktow stycznosci okregu wpisaneego w trojkat o bokach 3, 4, 5 do bokow tego trojkata. trojkat o takich bokach jest prostokatny.

zadanie: niech AB=4 BC=5 AC=3 punkty D, E, F to punkty stycznosci AD=AE=y BE=BF=z CD=CF=x x=3−y=5−z i z=4−y stad y=1 z=3 x=2 ale jak odpowiedziec na to pytanie w poleceniu ?

zadanie: ?

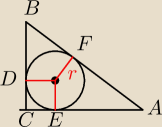
Mila: D,E,F punkty styczności okręgu odpowiednio z przyprostokątnymi o długościach |CB|=3,|CA|=4 i przeciwprostokątną |AB|=5. Obliczam r ( mozna inaczej) P=p*r, p=(3+4+5):2=6

1
	*3*4=6*r
2

r=1 Wystarczy rysunek i CE=CD=r=1 AE=AF=4−1=3 DB=BF=3−1=2 D,E,F punkty styczności okręgu odpowiednio z przyprostokątnymi o długościach |CB|=3,|CA|=4 i przeciwprostokątną |AB|=5.

zadanie: czyli konkretnie jak udzielic odpowiedzi na pytanie ?

Mila: Podac rozwiązanie , albo słownie w odległości 1 od wierzchołka kąta prostego, w odległości 2 od wierzchołka większego kata ostrego, w odległości 3 ..... Ja jestem za rysunkiem i rozwiązaniem. Nie wiem dokładnie jak wygląda cały problem, zadanie, test wyboru, krótka odpowiedź?

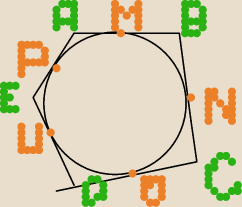
zadanie: Pięć kolejnych boków wielokąta opisanego na okręgu ma długości a, b, c, d, e (z zachowaniem kolejności). Wykazać, że wówczas b+d<a+c+e.

zadanie: zaraz napisze rozwiazanie

Mila: Litery na rysunku piszesz tak: klikasz ikonkę T, następnie klikasz na rysunku w którym miejscu ma być litera i wpisujesz z klawiatury..

zadanie: M, N, O, U, P punkty stycznosci AB=a BC=b CD=c DE=d EA=e oraz AM=AP=x MB=BN=y NC=CO=t OD=DU=s UE=EP=m b+d<a+c+e czyli y+t+s+m<x+m+t+s+x+y 0<2x; x>0 koniec dowodu dobrze?

zadanie: ok dziekuje

Mila: Punkty styczności okręgu z ramionami kata są jednakowo odległe od wierzchołków tego kata. Możesz końcowe rozwiązanie zapisać tak: x>0, y>0,m>0,t>0, s>0 b+d=y+t+s+m a+c+e=x+m+t+s+x+y=(y+t+s+m)+2x=b+d+2x>b+d ⇔ b+d<a+c+e

zadanie: ok dziekuje

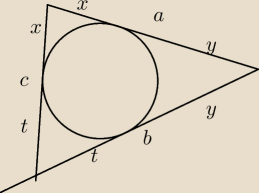
zadanie: Trzy kolejne boki wielokąta opisanego na okręgu mają długości a, b, c (z zachowaniem kolejności). Jaki warunek muszą spełniać a, b, c aby było to możliwe? tego nie umiem

Mila: Tak samo jak przedtem i próbuj porownać sumy i jeden bok a+b i c czy można wyciągnąć jakiś wniosek? a+c i b b+c i a

zadanie:

zadanie: a+b=x+y+y+t=2y+c a+c=x+y+x+t=2x+y+t=2x+b b+c=y+t+x+t=2t+x+y=2t+a

zadanie: czyli a+b=2y+c>c a+c=2x+b>b b+c=2t+a>a o to chodzilo?

zadanie: ?

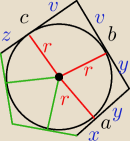
Mila: Raczej chodziło o wielokąt o większej liczbie boków, dla Δ sprawa jest oczywista. Rozwiąż.

zadanie: a=x+y b=y+v c=z+v

Mila: Dalej, ustaw warunek.

zadanie: przykro mi ale nie wiem

Mila: 1) a+b=x+y+y+v i c=z+v nie można wyciągnąć wniosku o związku a+b i c 2) a+c=x+y+z+v i b=y+v⇒a+c=b+x+z>b⇔a+c>b 3) b+c=y+v+z+v i a =x+y nie można wyciągnąć wniosku o związku b+c i a odp. a+c>b

zadanie: dziekuje bardzo

zadanie: jutro jeszcze chcialbym wrocic do zadania z wczoraj z 20:16

zadanie: wczesniej napisalem, ze dla n=5 tak bo wydaje mi sie, ze kazdy pieciokat wpisany w okrag i majacy katy rownej miary jest foremny podobnie dla n=6 bo nie umiem znalezc przykladu, ze tak nie jest

Mila: Dobrze.

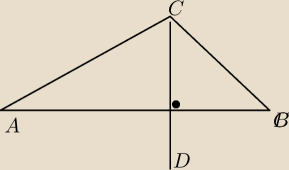
zadanie: Na płaszczyznie dany jest trójkat ABC. Ile co najwyzej moze istniec takich punktów D róznych od C, ze proste AB i CD sa prostopadłe, a przy tym <)ACB =<)ADB ? mam do tego rozwiazanie ale nie jest ono dla mnie wystarczajaco jasne odp.3 Z równosci katów wynika, ze punkt D lezy na tym łuku AB okregu opisanego na trójkacie ABC, który zawiera punkt C lub na odbiciu symetrycznym tegoz łuku wzgledem prostej AB (zrób rysunek w przypadku, gdy łuk jest wiekszy od półokregu). Figura bedaca suma tych dwóch łuków ma z prosta prostopadła do prostej AB co najwyzej 4 punkty wspólne. punkt D na rysunku jest tym punktem symetrycznym wiec jest na pewno taki 1 punkt D a jeszcze moga byc 2.

zadanie: rysunek sam zrobilem (nie bylo w rozwiazaniu)

zadanie: ?

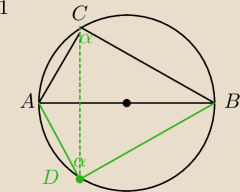
Mila: Tu chodzi o różne położenie punktu D, w zależności od rodzaju Δ. 1) ΔABD symetryczny do ΔABC ∡ACB=∡ADB=90^o

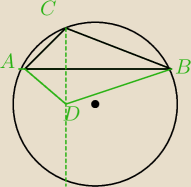
Mila: 2) ΔABC −Δrozwartokątny ∡C− kat rozwarty ΔABD symetryczny do ΔABC względem prostej AB ∡ACB=∡ADB D leży wewnątrz okręgu opisanego na Δ

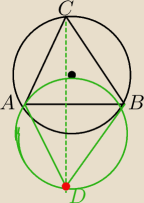
Mila: 3) ΔABD symetryczny do ΔABC względem prostej AB ∡ACB=∡ADB Punkt D leży poza okręgiem opisanym na ΔABC.

zadanie: dziekuje bardzo