Pazdro III 4.57h
pppp:
a=
1−√52
b=
1+√52
W prostokątnym układzie współrzędnych zaznacz zbiór tych punktów płaszczyzny, których
współrzędne spełniają poniższe warunki
log
y+1(x
2−x)>log
2y+1(x
2−x), gdzie y∊(−1,0)
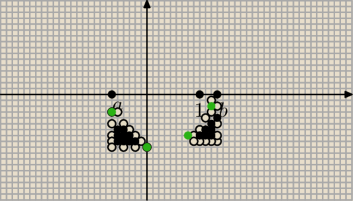
Wyszło mi
coś takiego jak wyżej , z tym, że te kropki od zielonej do zielonej "górą" przypominają u mnie
fragment paraboli x
2−x−1, tylko nie umiem tego tutaj narysować. W zbiorze jest odpowiedź co
najmniej podobna, nie jestem tylko pewna czy nie jest to tam jednak bardziej f.liniowa, ciężko
powiedzieć, wiec prosiłabym kogoś o sprawdzenie
wredulus_pospolitus:
niech: a=log
y+1(x
2−x)
a > a
2 <=> a
2−a < 0 <=> a*(a−1) < 0 <=>
I) a>0
wtedy a∊(0,1)
0<log
y+1(x
2−x)<1
skoro y∊(−1,0) to y+1∊(0,1) czyli:
1> (x
2−x) > y+1
1> x
2−x <=> x
2−x−1<0 (mamy wykres <zielone linie)
x
2−x>y+1 <=> x
2−x−1>y (fioletowe przerywane)
II) analogicznie
i w sumie wychodzi dobrze, miejsca zerowe paraboli dobrze wyznaczone ... jest ok