Sprawdzam 5-latek: bezendu Jak idzie z geometria ? czy sledzisz te zadania z ciagami dla Piotr10

bezendu: Witaj 5−latek planimetria coraz lepiej. Nie ma porównania z tym co było na początku a co jest teraz, ale jeszcze długa droga A zadania przeglądałem

5-latek: jak zadania z ciagow. Podobaly sie ? To teraz dla Ciebie z planimetrii Wyznacz dlugosc srodkowej trojkata ABC o bokach a b i c poprowadzonej z wierzcholka A

bezendu: podobały się

bezendu: z twierdzenia cosinusów ?

zm:

	1
s=		√2b2+2c2−a2
	4

zm: pomyłka,ma być

	1
s=		√2b2+2c2−a2
	2

bezendu: i Eta rozwiązała

zm: ?

bezendu: Dobrze wiemy, że to Ty Eta

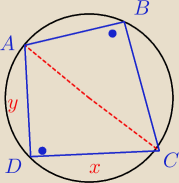
Piotr 10: bezendu masz coś ode mnie W okrąg o promieniu długości 10 wpisano czworokąt ABCD w taki sposób, że przekątna AC jest średnicą tego okręgu i tworzy z bokiem AB kąt 45⁰, a z bokiem AD kąt 30⁰. Oblicz długość przekątnej BD tego czworokąta oraz jego pole.

bezendu: Piotr nie prosiłem o zadanie ale jak już napisałeś, to trzeba zrobić

Piotr 10: pamiętam te zadanie, musisz zauważyć pewną rzecz i będzie z górki

bezendu: to będą dwa trójkąty prostokątne skoro przeciwprostokątna opiera się na średnicy ?

Piotr 10: Tak ten czworokąt będzie składał się z dwóch trójkątów prostokątnych i po zadanku już

zm: 1/ dwa trójkąty prostokątne P= 2/ tw. Ptolemeusza |BD|=

bezendu: AC=10 AB=5√2 AC=5√2 P=25

	x
sin30=
	AC

1		x
	=
2		10

2x=10 x=5

	y
sin60=
	10

√3		y
	=
2		10

2y=10√3 y=5√3

	1		25√3
P=		*5*5√3=
	2		2

	50+25√3
P=
	2

ok ?

Piotr 10: AC nie powinno równać się 20 przypadkiem ?

bezendu: a no zaraz będzie korekta ale dla AC=10 dobrze policzyłem ?

zm: z tw. Ptolemeusza : |AC|*|BD|= |AD|*|BC|+|AB|*|DC| |BD|=

tim: Ktoś tu chyba ucieka.

Piotr 10: Policz, gdy AC=20 i wtedy sprawdzę

bezendu: Rysunek tak jak post 19:32 AC=20 AB=10√2 BC=10√2 P_ABC=100 j² x=10 y=10√3 P_ADC=50√3 j² P=50(2+√3)j²

bezendu: tim

Piotr 10: Tak teraz zgadza się . Jeszcze przekątna BD została do policzenia

asdf: bezendu, z takim wsparciem to matura rozszerzona na 100% w Twoich rekach

bezendu: 20|BD|=10√3*10√2+10√2*10 20|BD|=100√6+100√2

	100(√6+√2)
|BD|=		=5(√6+√2)
	20

Piotr 10: A inny sposób ?

bezendu: na policzenie |BD| ?

Piotr 10: Tak

zm: |BD|= 5√2(1+√3) [j]

bezendu: Nie mam pomysłu na razie

Piotr 10: Na samym początku w tym poście wspomniałeś coś o tym − taka podpowiedź

bezendu: trójkąt prostokątny

Piotr 10: A nie twierdzenie cosinusów?

bezendu: a o to Ci chodzi to też by się dało chyba

Piotr 10: Na pewno by się dało . Tylko byś musiał wyliczyć ile to jest cos75⁰ . np.

	√3		√2		1		√2
cos(300+450)=cos300*cos450−sin300*sin450=		*		−		*		=
	2		2		2		2

	√6		√2		√6−√2
=		−		=
	4		4		4

5-latek: Masz jeszce dwa ode mnie .i na razie starczy. jesli przez s₁,s₂ s₃ oznaczymy dlugosci srodkowych trojkata a prze a b ic dlugosci bokow trojkata to wykaz z e w dowolnym trojkacie zachodzi zwiazek

	s12+s22+s32		3
		=
	a2+b2+c2		4

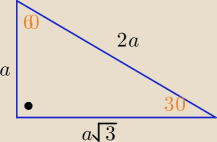
Zadanie nr2 dla rozluznienia . Czy istnieje trojkat prostokatnyz katem ostrym 30stopni ktorego dlugosci bokow sa liczbami naturalnymi

bezendu: OK dziękuje za zadanie

bezendu: 5−latek już miałem iść 2) istnieje taki trójkąt

Piotr 10: Chyba nie istnieje taki trójkąt prostokątny, ale tak na szybko mi się zdaję

zm: a∊N+ Wniosek ................

bezendu: nie istnieje

zm:

Piotr 10: Właśnie to od razu przyszło do głowy, że jeżeli jest trójkąt prostokątny i miara kąta ostrego to 30⁰ to jedna przyprostokątna przeciwległa do kąta alfa wynosi a, a więc przeciwprostokątna będzie 2a. A drugą przyprostokątna z tw.Pitagorasa wyjdzie, że równa się a√3

bezendu: I co zm to może nie Eta a w którymś poście bardzo się dziwiłaś

zm: ?

bezendu:

5-latek: bezendu to usmiales sie troche przy tym zadaniu?

bezendu: nawet się nie zastanawiałem tylko napisałem że jest a tym czasem już muszę uciekać dziękuje za zainteresowanie z Twojej strony