Każdy z boków trójkąta o polu 242 Problemek: Każdy z boków trójkąta o polu 242cm² podzielonzo na trzy części w stosunku 1:9:1. Oblicz pole sześciokąta, którego wierzchołkami są punkty podziału boków. Prosił bym też o wytłumaczenie w miarę proste tego zadania za co Dziękuje.

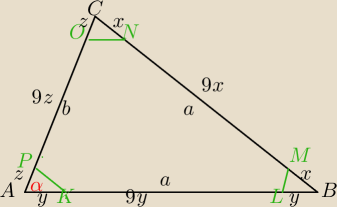
Mila: P_KLMNOP=P_Δabc−(P_ΔONC+P_ΔLMB+P_KPA)

	1x		1
ΔONC∼ΔABC w skali k=		=
	11x		11

Stosunek pól figur podobnych jest równy kwadratowi skali podobieństwa⇔

PΔONC		1		1
	=(		)2=
PΔABC		11		121

	1
PΔONC=		*242=2
	121

Analogicznie: P_ΔLMB=2 P_ΔKPA=2 P_KLMNOP=242−(2+2+2)=236 ========================= II sposób

	1
PΔABC=		*a*b*sinα
	2

	1
z=		b
	11

	1
y=		a
	11

	1		1		1		1
PΔKPA=		*z*y=		*		b*		a=
	2		2		11		11

	1		1		1
=		*(		a*b*sinα)=		*242=2
	121		2		121

Analogicznie można obliczyc ,że P_ΔONC=2 P_ΔLMB=2

Problemek: Bardzo dziękuje!

Mila: