funkcje
zadanie: | | 1 | |
[x+ |
| ], czyli czesc calkowita liczby rzeczywistej |
| | 2 | |
dobrze?
15 sie 21:04
Eta:
dobrze
15 sie 21:06
zadanie: dziekuje
15 sie 21:17
Eta:

15 sie 21:17
zadanie: a teraz mam pytanie
| | 1 | |
jak narysowac wykes tej funkcji f(x)=I[x+ |
| ]−xI ? |
| | 2 | |
15 sie 21:19
zadanie: co mam po kolei rysowac?
15 sie 21:43
15 sie 22:01
Mila:
Rozważ wartości funkcji w przedziale , zauważysz pewną prawidłowość.
<−1,1>
dla argumentów
| | 1 | |
f(−1)=|[−1+ |
| ]−(−1)|=|−1+1|=0 itd |
| | 2 | |
16 sie 00:51
16 sie 14:42
16 sie 14:49
zadanie: jest symetryczna wzgledem osi OY
16 sie 14:55
zadanie:
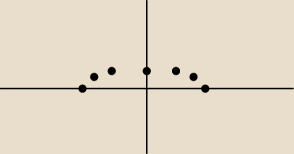
16 sie 15:00
zadanie: czy o to chodzilo?
16 sie 15:43
Mila:
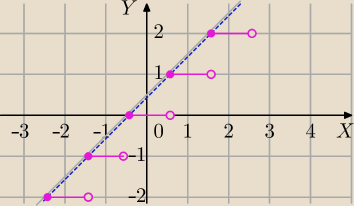
No to po kolei:
Liczymy:
| | 5 | | 5 | | 1 | | 5 | | 1 | |
f(− |
| )=| [− |
| + |
| ]−( |
| ))|= |
| |
| | 2 | | 2 | | 2 | | 2 | | 2 | |
| | 3 | | 3 | | 1 | | 3 | | 1 | |
f(− |
| )=|[− |
| + |
| ]− |
| |= |
| |
| | 2 | | 2 | | 2 | | 2 | | 2 | |
Itd
| | 1 | |
wykres f(x)=[x+ |
| ]−x] będzie na drugim wpisie, poczekam trochę na ewentualny Twój |
| | 2 | |
wykres.
16 sie 15:54
zadanie:
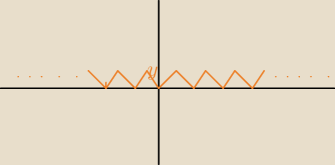
wydaje mi sie, ze to bedzie tak:
ladniej nie umiem
16 sie 16:58
zadanie: poczekam na sprawdzenie
16 sie 16:59
Mila:
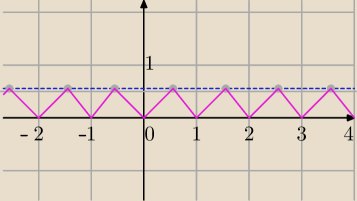
Dobrze.
Narysuję z jednostkami.
Narysuj wykres
f(x)=[x+2]
16 sie 17:21
zadanie:
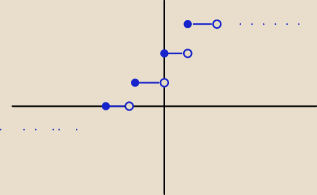
wydaje mi sie, ze bedzie tak
16 sie 18:39
zadanie: | | 1 | |
majac wykres funkcji f(x)=I[x+ |
| ]−xI jak narysowac wykres funkcji f1(x)=f(2x)? na |
| | 2 | |
poczatek chcialbym zapisac wzor tej funkcji f
1(x).
| | 1 | |
f1(x)=I[2x+ |
| ]−2xI czy dobrze jest on zapisany? |
| | 2 | |
16 sie 18:43
Mila: Wyglada dobrze
Układ wsp. możesz rysować klikając na ikonkę pod elipsą.
16 sie 18:43
Mila:
Do 18:43
"Zagęszczony " .
Analogia sin(x) i sin(2x).
16 sie 18:54
zadanie: | | 1 | |
to chyba bedzie tak: f1(x)=I2([x+ |
| ]−x)I=I[2x+1]−2xI ? |
| | 2 | |
16 sie 19:09
Mila:
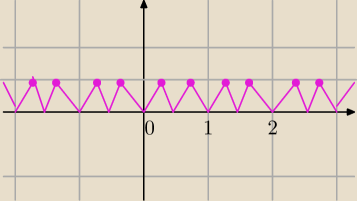
| | 1 | |
f(2x)=g(x)=|[2x+ |
| ]−2x| |
| | 2 | |
| | 1 | | 1 | | 1 | | 1 | | 1 | | 1 | |
g( |
| )=|[2* |
| + |
| ]−2* |
| |=|1− |
| |= |
| |
| | 4 | | 4 | | 2 | | 4 | | 2 | | 2 | |
| | 1 | | 1 | | 1 | | 1 | | 3 | |
g( |
| )=|[2* |
| + |
| ]−2* |
| |=|[ |
| ]−1|=0 |
| | 2 | | 2 | | 2 | | 2 | | 2 | |
Krzywo wyszło, ale chyba wiesz o co chodzi.
Zaraz usunę ten wykres.
16 sie 19:33
16 sie 21:07
zadanie: czyli jezeli jest f(2x) to za x wstawiam 2x tak?
16 sie 21:07
Mila: Tak.
Rysowałes wykresy?
| | 1 | |
sin(2x), cos(2x), sin (3x), sin ( |
| x) |
| | 2 | |
16 sie 21:11
zadanie: tak
| | 1 | |
jak jest 2x to wykres staje sie wezszy a |
| x to wykres staje sie szerszy |
| | 2 | |
16 sie 21:13
Mila: 
16 sie 21:16
zadanie: | | 1 | | 1 | | 1 | | 1 | | 1 | |
f2(x)=f( |
| x) czyli za x wstawiam |
| ; f2(x)=I[ |
| x+ |
| ]− |
| xI |
| | 2 | | 2 | | 2 | | 2 | | 2 | |
| | 1 | |
f3(x)=2f(x); f3(x)=2I[x+ |
| ]−xI |
| | 2 | |
dobrze?
16 sie 21:17
Mila: Zgadza się.
16 sie 21:43
zadanie: | | 1 | | 1 | |
a jak bedzie f4(x)=f(x+ |
| ) to za x mam wstawic x+ |
| czyli |
| | 4 | | 4 | |
| | 1 | | 1 | | 1 | | 3 | | 1 | |
f4(x)=I[x+ |
| + |
| ]−( x+ |
| )I=I[x+ |
| ]−x− |
| I |
| | 4 | | 2 | | 4 | | 4 | | 4 | |
| | 1 | |
f5(x)=5f(x)+3x; f5(x)=5I[x+ |
| ]−xI+3x |
| | 2 | |
a czy te przyklady sa dobrze?
16 sie 22:06
Mila:
Tak.
16 sie 22:17
zadanie: dziekuje
16 sie 22:40
zadanie: chcialbym jeszcze zapytac bo sie tak zastanawiam jak mam napisac wzor funkcji f
1(x)=f(2x) to
| | 1 | |
dlaczego nie moge napisac f1(x)=I[2x+1]−2xI tylko f1(x)=I2x+ |
| ]−2xI ? |
| | 2 | |
17 sie 10:16
zadanie: ?
17 sie 23:05
Mila:
f(2x) oznacza, że za argument wstawiasz 2x.
17 sie 23:11
zadanie: ok
dziekuje
17 sie 23:33
zadanie: funkcja nierosnaca, niemalejaca to inaczej stala?
17 sie 23:34
18 sie 00:00
zadanie: zapytalem dlatego, ze robilem takie zadanie, w ktorym trzeba bylo okreslic czy funkcja jest
parzysta, nieparzysta, monotoniczna.
i np. y=5 jest to funkcja parzysta i stala a w odp. bylo, ze jest to funkcja parzysta,
nierosnaca, niemalejaca. dlatego zapytalem sie czy jezeli funkcja jest nierosnaca, niemalejaca
to czy oznacza to, ze jest stala.no bo tak mozna wywnioskowac.
18 sie 12:01
Aga1.:
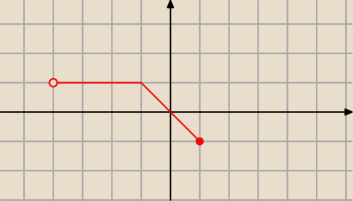
Oto przykładowy wykres funkcji nierosnącej.
Nierosnąca tzn. malejąca lub stała.
18 sie 12:29
zadanie: no tak ale jak jest niemalejaca i nierosnaca to znaczy, ze jest stala?
18 sie 12:57
zadanie: ?
18 sie 18:18
18 sie 18:36
zadanie: ok
dziekuje
18 sie 19:15
zadanie: funkcja rosnaca badz malejaca ma dokladnie 1 rozwiazanie
i w rownaniu typu √x7+x+7=3 a wlasciwie w rozwiazaniu jest taki komentarz, ze funkcja
x7+x+7 jest rosnaca czyli ma jedno rozwiazanie x=1. ale skad mam wiedziec, ze ta funkcja jest
rosnaca?
18 sie 19:18
Mila:
Źle to przepisałeś, co to znaczy ,że funkcja ma jedno rozwiązanie?
Może jedno miejsce zerowe?
Równanie ma jedno rozwiązanie.
Pochodna funkcji pod pierwiastkiem
f'(x)=x6+1>0 ⇔funkcja jest rosnąca dla x∊R
18 sie 20:03
Mila: Zbadaj z definicji, że funkcja jest rosnąca.
18 sie 20:56
zadanie: f(x)=x7+x+7
x1−x2<0
f(x1)−f(x2)=x17+x1+7−x27−x2−7=x17−x27+x1−x2=
=(x1−x2)(x16+x15x2+x14x22+x13x23+x12x24+x1x25+x26)+(x1−x2)
wyrazenie x1−x2<0 a wyrazenie
(x16+x15x2+x14x22+x13x23+x12x24+x1x25+x26) jaki ma znak?
18 sie 22:12
Mila:
Może tak.
x1<x2
to
x17<x27
Nieparzysta potęga nie zmienia znaku potęgowanej liczby.
18 sie 22:54
zadanie: f(x1)−f(x2)=(x17−x27)+(x1−x2)
oba te wyrazenia sa mniejsze od zera wiec f(x1)−f(x2)<0 stad ta funkcja jest rosnaca dobrze?
19 sie 16:41
zadanie: ?
19 sie 17:07
Mila: 
19 sie 20:16


 No to po kolei:
No to po kolei:
 wydaje mi sie, ze to bedzie tak:
wydaje mi sie, ze to bedzie tak:
 Dobrze.
Narysuję z jednostkami.
Narysuj wykres
f(x)=[x+2]
Dobrze.
Narysuję z jednostkami.
Narysuj wykres
f(x)=[x+2]
 wydaje mi sie, ze bedzie tak
wydaje mi sie, ze bedzie tak


 Oto przykładowy wykres funkcji nierosnącej.
Nierosnąca tzn. malejąca lub stała.
Oto przykładowy wykres funkcji nierosnącej.
Nierosnąca tzn. malejąca lub stała.
