znajdź tg kata BAD Paula: W trójkącie równobocznym abc na boku bc obrano punkt d taki. że stosunek pola trójkąta abd do pola trójkąta adc wynosi 2/5. Oblicz: a. stosunek długości odcinka BD do długości odcinka CD (ten podpunkt zrobiłam, wyszło 2/5) b. tg kąta BAD W podpunkcie b myślałam o przedstawieniu sin i cos BAD za pomocą a (moje oznaczenie boku dużego trójkąta) korzystając z twierdzenia cosinusów. W moim założeniu a skróciłoby się po podstawieniu do wzoru tgα=sinα/cosα jednak nie dokończyłam bo wychodziły brzydkie działania. Jest jakis inny sposób na to zadanie?

pigor: ... , innego sposobu niż z tw. cosinusów nie widzę, a wychodzi mi kolejno : AD= √39k i sin(∡BAD)=¹₁₃√13 ⇒ tg(∡BAD)=¹₆√3 . ...

pigor: ..., gdzie AD z tw. cosinusów, a sin(∡BAD) z tw. sinusów ...

Saizou :

2		PABD
	=
5		PACD

2P_ACD=5P_ABD

	1		1
2*		*a*(a−2x)*sin60=5*		*2x*a*sin60
	2		2

2a(a−2x)=10ax

2x		2a		2
	=		=		→10x=2a−4x→14x=2a→a=7x
a−2x		5a		5

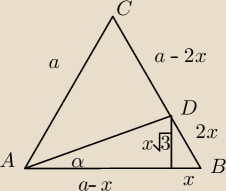
	x√3		x√3		x√3		√3
tgα=		=		=		=
	a−x		7x−x		6x		6

Paula: Dzięki bardzo za pomoc