bezwzględne
Kalumniatoris: Czy znacie jakąś stronę na której w przystępny sposób są wytłumaczone równania/nierówności z
wartością bezwzględną
typu:
|y−3|>=2+|x−3|
oraz jak wygląda rozwiązanie graficzne równań typu:
|x−2|=x−2
(chodzi mi o to jak to się zaznacza na osi/wykresie)
24 wrz 21:16
Bogdan:
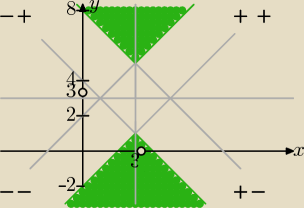
Dla x ≥ 3 i y ≥ 3: y − 3 ≥ 2 + x − 3 ⇒ y ≥ x + 2
Dla x < 3 i y ≥ 3: y − 3 ≥ 2 − x + 3 ⇒ y ≥ −x +8
Dla x < 3 i y < 3: −y + 3 ≥ 2 − x + 3 ⇒ y ≤ x − 2
Dla x ≥ 3 i y < 3: −y + 3 ≥ 2 + x − 3 ⇒ y ≤ −x + 4
24 wrz 22:01
Bogdan:
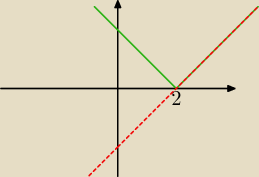
Jeden ze sposobów:
|x − 2| = x − 2
y = |x − 2|
y = x − 2
Dla x ≥ 2 linie pokrywają się, jest nieskończenie wiele rozwiązań.
Dla x < 2 brak rozwiązań
24 wrz 22:07
Kalumniatoris:
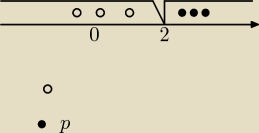
Dzięki nie pomyślałem o tym by popodstwiać y
metoda dużo przystępniejsza dla mnie
próbowałem obliczyć w osi
(o to minusy a te drugie to plusy)
|x−2|=2
x−2=2 v x−2=−2
x=2 v(i tu mi coś nie wychodzi x=4 lecz na osi logicznie wychodzi mi tylko tak jak
narysowałem
24 wrz 22:17
Bogdan:
A to pierwsze jest zrozumiałe ?
24 wrz 22:22
Kalumniatoris: ta część dla x>3 | x<3 to z powodu że jest |x−3| w równaniu?
a y>=3 | y<3 gdyż jest |y−3|
tą liczbę od której się bierze to <>
24 wrz 22:44
Bogdan:
Tak
24 wrz 22:46
 Dla x ≥ 3 i y ≥ 3: y − 3 ≥ 2 + x − 3 ⇒ y ≥ x + 2
Dla x < 3 i y ≥ 3: y − 3 ≥ 2 − x + 3 ⇒ y ≥ −x +8
Dla x < 3 i y < 3: −y + 3 ≥ 2 − x + 3 ⇒ y ≤ x − 2
Dla x ≥ 3 i y < 3: −y + 3 ≥ 2 + x − 3 ⇒ y ≤ −x + 4
Dla x ≥ 3 i y ≥ 3: y − 3 ≥ 2 + x − 3 ⇒ y ≥ x + 2
Dla x < 3 i y ≥ 3: y − 3 ≥ 2 − x + 3 ⇒ y ≥ −x +8
Dla x < 3 i y < 3: −y + 3 ≥ 2 − x + 3 ⇒ y ≤ x − 2
Dla x ≥ 3 i y < 3: −y + 3 ≥ 2 + x − 3 ⇒ y ≤ −x + 4
 Jeden ze sposobów:
|x − 2| = x − 2
y = |x − 2|
y = x − 2
Dla x ≥ 2 linie pokrywają się, jest nieskończenie wiele rozwiązań.
Dla x < 2 brak rozwiązań
Jeden ze sposobów:
|x − 2| = x − 2
y = |x − 2|
y = x − 2
Dla x ≥ 2 linie pokrywają się, jest nieskończenie wiele rozwiązań.
Dla x < 2 brak rozwiązań
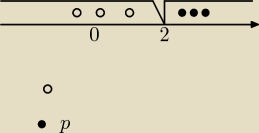 Dzięki nie pomyślałem o tym by popodstwiać y
metoda dużo przystępniejsza dla mnie
próbowałem obliczyć w osi
(o to minusy a te drugie to plusy)
|x−2|=2
x−2=2 v x−2=−2
x=2 v(i tu mi coś nie wychodzi x=4 lecz na osi logicznie wychodzi mi tylko tak jak
narysowałem
Dzięki nie pomyślałem o tym by popodstwiać y
metoda dużo przystępniejsza dla mnie
próbowałem obliczyć w osi
(o to minusy a te drugie to plusy)
|x−2|=2
x−2=2 v x−2=−2
x=2 v(i tu mi coś nie wychodzi x=4 lecz na osi logicznie wychodzi mi tylko tak jak
narysowałem