Zadanka Dzikuniii: Czy mógłby mi ktoś wytłumaczyć (tak porządne w prostym języku) jak rozwiązać te zadanka gdyż nie wiem z której strony i jak ma je ugryźć. Pozdrawiam

	x+2		y−1		2
1.Napisać równanie płaszczyzny π przechodzącej przez prostą l1:		=		=
	1		2		−3

	x−1		y+2		2
równoległej do l2:		=		=
	5		−3		1

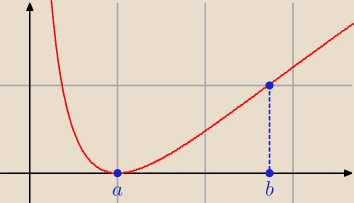
2.Obliczyć pole obszaru ograniczonego krzywą y=ln²x, osia OX, prostymi x=a,x=b, gdzie a jest odciętą punktum w którym jest ekstremum, a b − odcięta punktu przegięcia.

Trivial:

	lnx		1−lnx
2. y = ln2x, y' = 2		, y'' = 2*
	x		x2

Z porównań pochodnych do zera mamy: a = 1, b = e. Pole wynosi: P = ∫₁^e ln²x dx = [xln²x]₁^e − ∫₁^e 2lnxdx = e − 2([xlnx]₁^e − ∫₁^e dx) = e − 2e + 2(e−1) = e − 1

Trivial: Na samym końcu powinno oczywiście być P = e − 2

Trivial: A w pierwszym zadaniu to nie są równania prostych. Prawdopodobnie po prawej stronie równania ma być z zamiast 2.

Dzikuniii:

	z		z
Poprawka do zad1. powinno być		w l1 i		w l2.
	−3		1

Dzikuniii: Mógłbyś mi jeszcze wytłumaczyć jak zrobiłeś zadanie 2gie? W zadaniu 1 prawdopodobnie będzie schemat i wzory.

Trivial: Znajdujesz punkty a i b opisane w zadaniu poprzez przyrównanie pierwszej i drugiej pochodnej do zera (ekstremum i punkt przegięcia). Obszar ograniczony opisany w treści zadania to obszar pod wykresem funkcji ln²x (geometryczna definicja całki). Żeby policzyć ile wynosi pole tego obszaru wystarczy policzyć całkę ∫_a^b ln²x dx.

AS: Zad 1 Wektory kierunkowe prostych: w1 = [1,2,−3] , w2 = [5,−3,1] Wektor kierunkowy płaszczyzny: w = w1 x w2 = [1,2,−3] x [5,−3,1] = [−7,−16,−13] Obieram dowolny punkt na pierwszej prostej np. P(−1,3,3) Równanie płaszczyzny: −7*(x + 1) − 16*(y − 3) − 13*(z − 3) = 0 7*x + 16*y + 13*z − 80 = 0 (Odp)

pigor: ..., ad. zad.2. prosta l₁ ma wektor kierunkowy u=[1,2,−3] i M=(−2,1,0)∊l₁; prosta l₂ ma wektor kierunkowy v=[5,−3,1] i N=(1,−2,0)∊l₁, a wektor MN=[3,−3,0] iloczyn mieszany wektorów |3 −3 0| (MNxu)*v= |1 2 −3|= 6+45=27+3= 45−23≠ 0, to wektory te są niekomplanarne, czyli |5 −3 1| proste l₁ i l₂ są skośne, zatem iloczyn wektorowy : |i j k| uxv= |1 2 −3|= 2i−15j−3k−10k−9i−j= −7i−16j−13k= [−7,−16−13]= −[ 7,16,13 ] − wektor |5 −3 1| normalny szukanej płaszczyzny π i z warunków zadania, M=(−2,1,0)∊l₁∊π, zatem π: 7(x+2)+16(y−1)+13(z−0)=0 ⇔ 7x+14+16y−16+13z=0 ⇔ 7x+16y+13z−2=0. ...

pigor: ... oczywiście jest to ad. zad.1.

AS: Korekta do mojego rozwiązania Błędnie przyjąłem w pierwszym równaniu ... = z/3 zamiast z/(−3) Obrany punkt ma postać: P(−1,3,−3) Wtedy równanie płaszczyzny: 7*x + 16*y + 13*z − 2 = 0. Pardon.