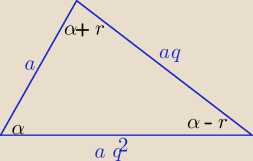
 α−r,α, α+r −−− miary kątów tworzą ciąg arytmetyczny
α−r+α+α+r=180o ⇒ α=60o
na przeciw większego kąta leży większy bok
to: a , aq, aq2 −−− długości boków tworzą ciąg geometryczny i a>0 i q>0
z tw. kosinusów:
(aq)2=a2+(aq2)2−2a*aq2*cos60o /: a2 , bo a≠0= 1
q2=1+q4−q2 ⇒ q4−2q2+1=0 ⇒(q2−1)2=0 ⇒ ......... q=1
to długości boków są : a,a,a −−− zatem trójkąt jest równoboczny
α−r,α, α+r −−− miary kątów tworzą ciąg arytmetyczny
α−r+α+α+r=180o ⇒ α=60o
na przeciw większego kąta leży większy bok
to: a , aq, aq2 −−− długości boków tworzą ciąg geometryczny i a>0 i q>0
z tw. kosinusów:
(aq)2=a2+(aq2)2−2a*aq2*cos60o /: a2 , bo a≠0= 1
q2=1+q4−q2 ⇒ q4−2q2+1=0 ⇒(q2−1)2=0 ⇒ ......... q=1
to długości boków są : a,a,a −−− zatem trójkąt jest równoboczny