zaliczenie xzallizx: Mam do zrobienia 4 zadan z bryl obrotowych.. A niestety matmy nie umiem. Prosze o pomoc Będe bardzo wdzięczny zad1 Przekątna przekroju osiowego walca ma dlugosc 40cm i tworzy z podstawa walca kat α taki, ze tgα=3/4. Oblicz V i Pc zad2 Kąt rozwarcia stozka ma miare 60stopni, a pole jego powierzchni bocznej wynosi 16Ω cm2 . oblicz V i Pc zad.3 Z wycinka kola o promieniu 10cm chcemy utworzyc powierzchnie boczna stozka, ktorego wysokosc ma byc rowna 8cm. Jaki powinien byc kąt środkowy tego wycinka zad4 Trapez rownoramienny o podstawach 6 i 10 oraz kacie ostrym 60stopni obraca sie wokol dluzszej podstawy. Oblicz objetosc o pole powierzchni calkowitej podstawy bryly

Godzio: Rysunki chyba potrafisz zrobić, definicje funkcji trygonometrycznych powinieneś znać, więc: Zad. 1

	3		H		3		H		3
tgα =		, ale wiemy, że tgα =		⇒		=		⇒ 3r = 2H ⇒ H =		r
	4		2r		4		2r		2

Teraz z Twierdzenia Pitagorasa:

	9		13
402 = r2 + H2 ⇒ 402 = r2 +		r2 ⇒ 402 =		r2 / √
	4		4

	√13		80		120
40 =		r ⇒ r =		⇒ H =
	2		√13		√13

Wystarczy teraz podstawić do wzoru na V i P_c Zad. 2 Skoro kąt rozwarcia ma 60^o to mamy w przekroju trójkąt równoboczny. ⇒ l = 2r P_b = 16π (nie wiem co to za omega się wkradła, chyba miało być π ) πrl = 16π /: π ⇒ 2r² = 16 ⇒ r² = 8 ⇒ r = 2√2 ⇒ l = 4√2 No i podstawianie do wzoru Zad. 3 H = 8 cm, R = 10 cm

	α
Pb = πrl = Pwycinka o kącie α =		* πR2
	360

	α
πrl =		* πR2, oczywiście R = l, zatem po uproszczeniu
	360

	α
r =		* R2 (r − promień podstawy stożka, l − tworząca stożka)
	360

Z Twierdzenia Pitagorasa (pamiętamy l = R ) r² + H² = l² ⇒ r² = R² − H² ⇒ r = 6

	α
Wstaw do równania r =		* R2 i wylicz α
	360

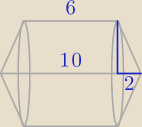Godzio: Zad. 4 Jak widać powstały nam dwa identyczne stożki i walec

10 − 6
	= 2 → wysokość stożka,
2

	r
tg60o =		⇒ r = 2√3 → promień podstawy stożka/walca
	2

	2		1		2
cos60o =		⇒		=		⇒ l = 4 (tworząca stożka)
	l		2		l

	1
V = Vw + 2Vs = π * (2√3)2 * 6 + 2 *		π * (2√3)2 * 2 = ...
	3

P_c = P_{boczne walca} + 2 * P_{boczne stożka} = ...

xzallizx: a moglbys zrobic te podstawienia zrobic, bo wogole nie znam wzorów prosze